练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用反证法证明命题：“已知为实数，则方程至少有一个实根”时，要做的假设是

    （A）方程没有实根（B）方程至多有一个实根

    （C）方程至多有两个实根（D）方程恰好有两个实根



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设函数，其中，

    （1）求函数的定义域D；（用区间表示）

    （2）讨论在区间D上的单调性；

    （3）若，求D上满足条件的的集合。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某企业有甲、乙两个研发小组，为了比较他们的研发水平，现随机抽取这两个小组往年

    研发新产品的结果如下：

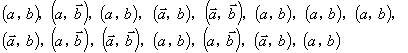
    其中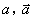分别表示甲组研发成功和失败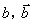；分别表示乙组研发成功和失败.

    （I）若某组成功研发一种新产品，则给改组记1分，否记0分，试计算甲、乙两组研

         发新产品的成绩的平均数和方差，并比较甲、乙两组的研发水平；

    （II）若该企业安排甲、乙两组各自研发一种新产品，试估算恰有一组研发成功的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


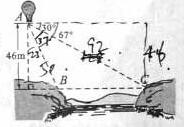
    如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为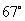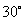，，此时气球的高是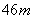，则河流的宽度BC约等于  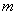     。（用四舍五入法将结果精确到个位。参考数据：，，，，）

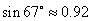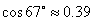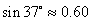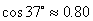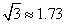    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆C：（）的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形。

    （1）求椭圆C的标准方程；

    （2）设F为椭圆C的左焦点，T为直线上任意一点，过F作TF的垂线交椭圆C于点P，Q。

    （i）证明：OT平分线段PQ（其中O为坐标原点）；

    （ii）当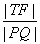最小时，求点T的坐标。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知满足约束条件当目标函数在该约束条件下取到最小值时，的最小值为

    （A）5（B）4（C）（D）2

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年浙江省杭州地区7校高三上学期期末模拟联考文科数学试卷（解析版） 题型：解答题

    （本题满分15分）已知函数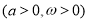的最大值为2，是集合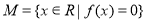中的任意两个元素，且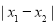的最小值为．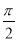

    （1）求函数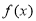的解析式及其对称轴；

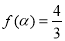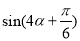    （2）若，求的值．

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年浙江省杭州地区7校高三上学期期末模拟联考理科数学试卷（解析版） 题型：解答题

    （本题满分15分）已知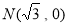，是平面上的两个定点，动点满足．

    （1）求动点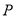的轨迹方程；

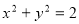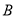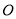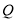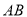    （2）已知圆方程为，过圆上任意一点作圆的切线，切线与（1）中的轨迹交于，两点，为坐标原点，设为的中点，求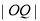长度的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年稳派新课程高三2月精品理科数学试卷（解析版） 题型：解答题

    （本题满分14分）已知函数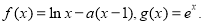

    （1）求函数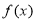的单调区间；

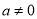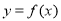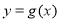    （2）当时，过原点分别作曲线和的切线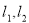，已知两切线的斜率互为倒数，证明：；

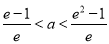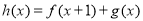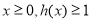    （3）设，当时，求实数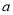的取值范围.

    查看答案和解析>>

    同步练习册答案