
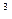 +3x
+3x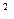 +ax+b)e
+ax+b)e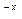 。
。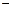 3 ,求f (x) 的单调区间;
3 ,求f (x) 的单调区间;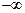 ,
,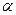 ),(2,
),(2,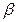 )上单调递增,在(
)上单调递增,在(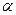 ,2),(
,2),(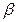 ,+
,+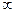 )上单调递减,证明:
)上单调递减,证明: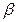 -
-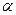 >6。
>6。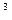 +3x
+3x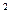 -3x-3)e
-3x-3)e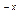 ,故
,故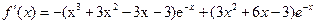 =
=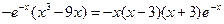 ……………………………………………………………………………………3分
……………………………………………………………………………………3分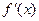 >0; 当-3<x<0或x>3时,
>0; 当-3<x<0或x>3时,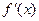 <0,
<0,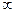 ,-3),(0,3)上单调递增,
,-3),(0,3)上单调递增,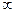 )上单调递减………………………………………………………. 6分
)上单调递减………………………………………………………. 6分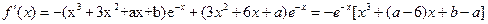
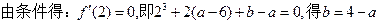 …………….……………8分
…………….……………8分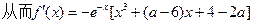
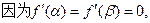
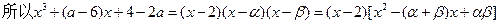
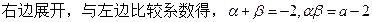 ……..…..…………….10分
……..…..…………….10分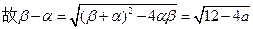 ………………………………………………..11分
………………………………………………..11分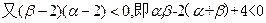 .
.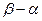 >6。………………………………………………………… 12分
>6。………………………………………………………… 12分

 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源:不详 题型:单选题
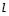 与直线3x-y+2=0平行,若数列
与直线3x-y+2=0平行,若数列 的前n项和为Sn,则S2009的值为( )
的前n项和为Sn,则S2009的值为( )A. | B. | C. | D.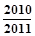 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
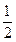 )上无零点,求a的取值范围.
)上无零点,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
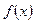 的定义域是
的定义域是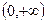 ,且对任意的正实数
,且对任意的正实数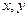 都有
都有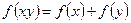 恒成立. 已知
恒成立. 已知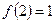 ,且
,且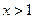 时,
时,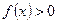 .
.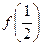 的值K]
的值K]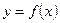 在
在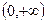 上的单调性,并给出你的证明
上的单调性,并给出你的证明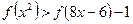 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com