
【题目】根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
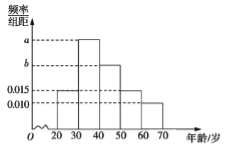
(1)已知中间三个年龄段的网上购票人数成等差数列,求![]() 的值;
的值;
(2)为鼓励大家网上购票,该平台常采用购票就发放酒店入住代金券的方法进行促销,具体做法如下:
年龄在![]() 岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率.
岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率.
【答案】(1)![]() ,
,![]() .(2)
.(2)![]()
【解析】
试题分析:(1)每个小长方形的面积等于对应概率,所有小长方形面积和为1,列式得![]() ,
,![]() ,解得
,解得![]() ,
,![]() .(2)先根据分层抽样得年龄在
.(2)先根据分层抽样得年龄在![]() 岁的有3人,其余年龄段的有2人,再确定金额总和为90元的情况:2个20元和1个50元,最后利用枚举法得从中随机抽取3人,可得到以下10种可能的结果;2个20元和1个50元包含6种可能的结果,因此概率为
岁的有3人,其余年龄段的有2人,再确定金额总和为90元的情况:2个20元和1个50元,最后利用枚举法得从中随机抽取3人,可得到以下10种可能的结果;2个20元和1个50元包含6种可能的结果,因此概率为![]()
试题解析:(1)依题意,![]() ,
,![]() ,
,
解得:![]() ,
,![]() .
.
(2)利用分层抽样的方式从1000位网上购票者中抽取5人,其中年龄在![]() 岁的有3人,其余年龄段的有2人,分别记为
岁的有3人,其余年龄段的有2人,分别记为![]() ,其中
,其中![]() 表示年龄在
表示年龄在![]() 岁的3人,
岁的3人,![]() 表示其余年龄段的2人.
表示其余年龄段的2人.
从中随机抽取3人,可得到以下10种可能的结果:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
若此3人获得代金券的金额总和为90元,则需2个20元和1个50元,记此事件为![]() ,则
,则![]() 包含的结果有
包含的结果有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6种
,共6种
故所求的概率![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两位数学老师组队参加某电视台闯关节目,共3关,甲作为嘉宾参与答题,若甲回答错误,乙作为亲友团在整个通关过程中至多只能为甲提供一次帮助机会,若乙回答正确,则甲继续闯关,若某一关通不过,则收获前面所有累积奖金.约定每关通过得到奖金2000元,设甲每关通过的概率为![]() ,乙每关通过的概率为
,乙每关通过的概率为![]() ,且各关是否通过及甲、乙回答正确与否均相互独立.
,且各关是否通过及甲、乙回答正确与否均相互独立.
(1)求甲、乙获得2000元奖金的概率;
(2)设![]() 表示甲、乙两人获得的奖金数,求随机变量
表示甲、乙两人获得的奖金数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网络购物已经被大多数人接受,随着时间的推移,网络购物的人越来越多,然而也有部分人对网络购物的质量和信誉产生怀疑。对此,某新闻媒体进行了调查,在所有参与调查的人中,持“支持”和“不支持”态度的人数如下表所示:
年龄 态度 | 支持 | 不支持 |
20岁以上50岁以下 | 800 | 200 |
50岁以 (含50岁) | 100 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“支持”态度的人中抽取了9人,求
个人,已知从持“支持”态度的人中抽取了9人,求![]() 的值;
的值;
(2)是否有99.9%的把握认为支持网络购物与年龄有关?
参考数据:
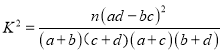 ,其中
,其中![]() ,
,
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中![]() 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
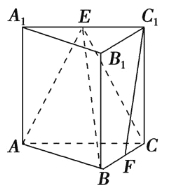
(1)求证:AB⊥平面B1BCC1; 平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔场鱼群的最大养殖量为![]() 吨,为保证鱼群的生长空间,实际的养殖量
吨,为保证鱼群的生长空间,实际的养殖量![]() 要小于
要小于![]() ,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量
,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量![]() (吨)和实际养殖量
(吨)和实际养殖量![]() (吨)与空闲率的乘积成正比(设比例系数
(吨)与空闲率的乘积成正比(设比例系数![]() ).
).
(1)写出![]() 与
与![]() 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)求鱼群年增长量的最大值;
(3)当鱼群年增长量达到最大值时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com