
【题目】如图,已知椭圆 ![]() (a>b>0)的左右顶点分别是A(﹣
(a>b>0)的左右顶点分别是A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),离心率为
,0),离心率为 ![]() .设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.
.设点P(a,t)(t≠0),连接PA交椭圆于点C,坐标原点是O.
(Ⅰ)证明:OP⊥BC;
(Ⅱ)若三角形ABC的面积不大于四边形OBPC的面积,求|t|的最小值.
【答案】解:(Ⅰ)由题意可知:a= ![]() ,e=
,e= ![]() =
= ![]() =
= ![]() ,则b=1,
,则b=1,
∴椭圆的标准方程: ![]() ,
,
设直线PA的方程y= ![]() (x+
(x+ ![]() ),
),
则 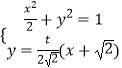 ,
,
整理得:(4+t2)x2+2 ![]() t2x+2t2﹣8=0,
t2x+2t2﹣8=0,
解得:x1=﹣ ![]() ,x2=
,x2= ![]() ,则C点坐标(
,则C点坐标( ![]() ,
, ![]() ),
),
故直线BC的斜率kBC=﹣ ![]() ,直线OP的斜率kOP=
,直线OP的斜率kOP= ![]() ,
,
∴kBCkOP=﹣1,
∴OP⊥BC;
(Ⅱ)由(Ⅰ)可知:四边形OBPC的面积S1= ![]() ×丨OP丨×丨BC丨=
×丨OP丨×丨BC丨= ![]() ,
,
则三角形ABC,S2= ![]() ×2
×2 ![]() ×
× ![]() =
= ![]() ,
,
由 ![]() ≤
≤ ![]() ,整理得:t2+2≥4,则丨t丨≥
,整理得:t2+2≥4,则丨t丨≥ ![]() ,
,
∴丨t丨min= ![]() ,
,
|t|的最小值 ![]() .
.
【解析】(Ⅰ)由a= ![]() ,椭圆的离心率e=
,椭圆的离心率e= ![]() =
= ![]() ,求得b,求得椭圆的标准方程,求得直线PA的方程,求得C点坐标,直线BC的斜率kBC=﹣
,求得b,求得椭圆的标准方程,求得直线PA的方程,求得C点坐标,直线BC的斜率kBC=﹣ ![]() ,直线OP的斜率kBC=
,直线OP的斜率kBC= ![]() ,则kBCkBC=﹣1,则OP⊥BC;(Ⅱ)分别求得三角形ABC的面积和四边形OBPC的面积,由题意即可求得|t|的最小值.
,则kBCkBC=﹣1,则OP⊥BC;(Ⅱ)分别求得三角形ABC的面积和四边形OBPC的面积,由题意即可求得|t|的最小值.


科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC= ![]() AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.
AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.
(1)求证:CM∥平面ABEF;
(2)求三棱锥D﹣ACF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}满足a1=1,且a1 , a2 , a5成等比数列.
(1)求{an}的通项公式;
(2)若bn=(﹣1)n ![]() (n∈N*),求数列{bn}的前n项和Sn .
(n∈N*),求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是以a为首项,q为公比的等比数列,数列{bn}满足bn=1+a1+a2+…+an(n=1,2,…),数列{cn}满足cn=2+b1+b2+…+bn(n=1,2,…).若{cn}为等比数列,则a+q=( )
A.![]()
B.3
C.![]()
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a2=6,a3+a6=27.
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn , 且Tn= ![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+ ![]() ﹣1,a∈R.
﹣1,a∈R.
(1)若关于x的不等式f(x)≤ ![]() x﹣1在[1,+∞)上恒成立,求a的取值范围;
x﹣1在[1,+∞)上恒成立,求a的取值范围;
(2)设函数g(x)= ![]() ,若g(x)在[1,e2]上存在极值,求a的取值范围,并判断极值的正负.
,若g(x)在[1,e2]上存在极值,求a的取值范围,并判断极值的正负.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y=2x2 , 直线l:y=kx+2交C于A,B两点,M是线段AB的中点,过M作x轴的垂线C于点N.
(1)证明:抛物线C在点N处的切线与AB平行;
(2)是否存在实数k使以AB为直径的圆M经过点N,若存在,求k的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com