考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用递推式即可得出;
(2)a
n+2=2a
n+1-a
n+2,可得(a
n+2-a
n+1)-(a
n+1-a
n)=2,即可证明;
(3)利用等差数列的通项公式与“累加求和”即可得出;
(4)由(2)可知:
=
=
[-],利用“裂项求和”即可得出.
解答:
(1)解:∵a
0=0,a
1=2,且对一切n∈N,有a
n+2=2a
n+1-a
n+2.
∴a
2=2a
1-a
0+2=2×2-0+2=6,
a
3=2a
2-a
1+2=2×6-2+2=12.
(2)证明:∵a
n+2=2a
n+1-a
n+2,
∴a
n+2-a
n+1=a
n+1-a
n+2,
化为(a
n+2-a
n+1)-(a
n+1-a
n)=2,
∴数列{a
n-a
n-1}为等差数列,且首项 a
1-a
0=2-0=2,公差为2.
(3)解:由(2)可得a
n-a
n-1=a
1-a
0+2(n-1)=2+2(n-1)═2n.
∴a
n=a
1+(a
2-a
1)+(a
3-a
2)+…+(a
n-a
n-1)=2+4+6+…++2n=
=n(n+1).
(4)证明:由(2)可知:
=
=
[-],
∴T
n=
+
+
+…+
=
[(-)+(-)+…+
(-)]=
[-]=
-<.
∴T
n<.
点评:本题考查了等差数列的通项公式及其前n项和公式、“累加求和”、“裂项求和”,考查了变形能力,考查了推理能力与计算能力,属于难题.



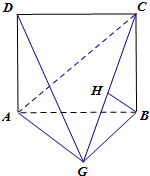 已知四棱锥G-ABCD,四边形ABCD是长为2a的正方形,DA⊥平面ABG,且GA=GB,BH⊥平面CAG,垂足为H,且H在直线CG上.
已知四棱锥G-ABCD,四边形ABCD是长为2a的正方形,DA⊥平面ABG,且GA=GB,BH⊥平面CAG,垂足为H,且H在直线CG上.