
| AЃЎ | ЕШБпШ§НЧаЮ | BЃЎ | ШёНЧШ§НЧаЮ | CЃЎ | ЖлНЧШ§НЧаЮ | DЃЎ | жБНЧШ§НЧаЮ |
ЗжЮі ИљОнЬѕМўНјааЯђСПЪ§СПЛ§ЕФдЫЫуЃЌвдМАИљОнЯђСПМгЗЈЁЂМѕЗЈКЭЪ§ГЫЕФМИКЮвтвхБуПЩЕУГі$\overrightarrow{BC}•\overrightarrow{AB}=0$ЃЌетбљБуПЩЕУГіШ§НЧаЮABCЕФаЮзДЃЎ
НтД№ НтЃК${\overrightarrow{AC}}^{2}=\overrightarrow{AB}•\overrightarrow{AC}+\overrightarrow{BA}•\overrightarrow{BC}+\overrightarrow{CA}•\overrightarrow{CB}$
=$\overrightarrow{AB}•\overrightarrow{AC}-\overrightarrow{AB}•\overrightarrow{BC}+\overrightarrow{AC}•\overrightarrow{BC}$
=$\overrightarrow{AB}•\overrightarrow{AC}+\overrightarrow{BC}•ЃЈ\overrightarrow{AC}-\overrightarrow{AB}ЃЉ$
=$\overrightarrow{AB}•\overrightarrow{AC}+\overrightarrow{BC}•\overrightarrow{BC}$ЃЛ
Ёр$\overrightarrow{AC}•\overrightarrow{AC}-\overrightarrow{AB}•\overrightarrow{AC}=\overrightarrow{BC}•\overrightarrow{BC}$ЃЛ
Ёр$\overrightarrow{BC}•\overrightarrow{AC}-\overrightarrow{BC}•\overrightarrow{BC}=0$ЃЛ
Ёр$\overrightarrow{BC}•\overrightarrow{AB}=0$ЃЛ
Ёр$\overrightarrow{BC}•\overrightarrow{AB}=0$ЃЛ
МДBCЁЭABЃЛ
ЁрЁїABCЮЊжБНЧШ§НЧаЮЃЎ
ЙЪбЁDЃЎ
ЕуЦР ПМВщЯђСПМгЗЈЁЂМѕЗЈМАЪ§ГЫЕФМИКЮвтвхЃЌвдМАЯђСПЪ§СПЛ§ЕФдЫЫуЃЌЯђСПДЙжБЕФГфвЊЬѕМўЃЎ


 вЛЯпУћЪІПкЫугІгУЬтЬьЬьСЗвЛБОШЋЯЕСаД№АИ
вЛЯпУћЪІПкЫугІгУЬтЬьЬьСЗвЛБОШЋЯЕСаД№АИ аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ
аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
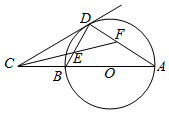 ШчЭМЃЌABЪЧдВOЕФжБОЖЃЌCЮЊABЕФбгГЄЯпЩЯвЛЕуЃЌЧаЯпCDНЛдВOгкЕуDЃЌЁЯACDЕФЦНЗжЯпЗжБ№НЛDBЃЌDAгкЕуEЃЌFЃЎ
ШчЭМЃЌABЪЧдВOЕФжБОЖЃЌCЮЊABЕФбгГЄЯпЩЯвЛЕуЃЌЧаЯпCDНЛдВOгкЕуDЃЌЁЯACDЕФЦНЗжЯпЗжБ№НЛDBЃЌDAгкЕуEЃЌFЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ГфЗжВЛБивЊЬѕМў | BЃЎ | БивЊВЛГфЗжЬѕМў | ||
| CЃЎ | ГфвЊЬѕМў | DЃЎ | МШВЛГфЗжгжВЛБивЊЬѕМў |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{b-c}{a}$ЃО0 | BЃЎ | $\frac{a}{c}$ЃМ$\frac{b}{c}$ | CЃЎ | $\frac{c-a}{ac}$ЃМ0 | DЃЎ | $\frac{{c}^{2}}{a}$ЃМ$\frac{{b}^{2}}{a}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌе§ЫФРтзЖS-ABCDЕФЕзУцБпГЄЮЊ2ЃЌEЃЌFЗжБ№ЮЊSAЃЌSDЕФжаЕуЃЎ
ШчЭМЃЌе§ЫФРтзЖS-ABCDЕФЕзУцБпГЄЮЊ2ЃЌEЃЌFЗжБ№ЮЊSAЃЌSDЕФжаЕуЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
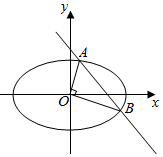 вбжЊЭждВCЃК$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЃЈaЃОbЃО0ЃЉЕФНЙОрЮЊ2$\sqrt{3}$ЃЌГЄжсГЄЮЊ4ЃЎ
вбжЊЭждВCЃК$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЃЈaЃОbЃО0ЃЉЕФНЙОрЮЊ2$\sqrt{3}$ЃЌГЄжсГЄЮЊ4ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | КсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф | |
| BЃЎ | КсзјБъЫѕЖЬЕНдРДЕФ$\frac{1}{2}$БЖЃЌзнзјБъВЛБф | |
| CЃЎ | знзјБъЩьГЄЕНдРДЕФ2БЖЃЌКсзјБъВЛБф | |
| DЃЎ | знзјБъЫѕЖЬЕНдРДЕФ$\frac{1}{2}$БЖЃЌКсзјБъВЛБф |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 17 | BЃЎ | 18 | CЃЎ | 19 | DЃЎ | 20 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com