
ЁОЬтФПЁПвбжЊ![]() ЪЧТњзуЯТСааджЪЕФЫљгаКЏЪ§
ЪЧТњзуЯТСааджЪЕФЫљгаКЏЪ§![]() зщГЩЕФМЏКЯЃКЖдШЮКЮ
зщГЩЕФМЏКЯЃКЖдШЮКЮ![]() ЃЈЦфжа
ЃЈЦфжа![]() ЮЊКЏЪ§
ЮЊКЏЪ§![]() ЕФЖЈвхгђЃЉЃЌОљга
ЕФЖЈвхгђЃЉЃЌОљга![]() ГЩСЂ.
ГЩСЂ.
ЃЈ1ЃЉвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЌХаЖЯ
ЃЌХаЖЯ![]() гыМЏКЯ
гыМЏКЯ![]() ЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌ
ЃЌ![]() ЪєгкМЏКЯ
ЪєгкМЏКЯ![]() ЃПШєДцдкЃЌЧѓ
ЃПШєДцдкЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЕФШЁжЕЗЖЮЇЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЖдгкЪЕЪ§![]() ЁЂ
ЁЂ![]()
![]() ЃЌгУ
ЃЌгУ![]() БэЪОМЏКЯ
БэЪОМЏКЯ![]() жаЖЈвхгђЮЊЧјМф
жаЖЈвхгђЮЊЧјМф![]() ЕФКЏЪ§ЕФМЏКЯ.
ЕФКЏЪ§ЕФМЏКЯ.
ЖЈвхЃКвбжЊ![]() ЪЧЖЈвхдк
ЪЧЖЈвхдк![]() ЩЯЕФКЏЪ§ЃЌШчЙћДцдкГЃЪ§
ЩЯЕФКЏЪ§ЃЌШчЙћДцдкГЃЪ§![]() ЃЌЖдЧјМф
ЃЌЖдЧјМф![]() ЕФШЮвтЛЎЗжЃК
ЕФШЮвтЛЎЗжЃК![]() ЃЌКЭЪН
ЃЌКЭЪН![]() КуГЩСЂЃЌдђГЦ
КуГЩСЂЃЌдђГЦ![]() ЮЊ
ЮЊ![]() ЩЯЕФЁАОјЖдВюгаНчКЏЪ§ЁБЃЌЦфжаГЃЪ§
ЩЯЕФЁАОјЖдВюгаНчКЏЪ§ЁБЃЌЦфжаГЃЪ§![]() ГЦЮЊ
ГЦЮЊ![]() ЕФЁАОјЖдВюЩЯНчЁБЃЌ
ЕФЁАОјЖдВюЩЯНчЁБЃЌ![]() ЕФзюаЁжЕГЦЮЊ
ЕФзюаЁжЕГЦЮЊ![]() ЕФЁАОјЖдВюЩЯШЗНчЁБЃЌЗћКХ
ЕФЁАОјЖдВюЩЯШЗНчЁБЃЌЗћКХ![]() ЃЛЧѓжЄЃКМЏКЯ
ЃЛЧѓжЄЃКМЏКЯ![]() жаЕФКЏЪ§
жаЕФКЏЪ§![]() ЪЧЁАОјЖдВюгаНчКЏЪ§ЁБЃЌВЂЧѓ
ЪЧЁАОјЖдВюгаНчКЏЪ§ЁБЃЌВЂЧѓ![]() ЕФЁАОјЖдВюЩЯШЗНчЁБ.
ЕФЁАОјЖдВюЩЯШЗНчЁБ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЪєгкМЏКЯ
ЪєгкМЏКЯ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉТд.
ЃЛЃЈ3ЃЉТд.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвбжЊЬѕМўЃЌЭЈЙ§ШЮШЁ![]() ЃЌжЄУї
ЃЌжЄУї![]() ГЩСЂЃЌЫЕУїfЃЈxЃЉЪєгкМЏКЯMЃЎЃЈ2ЃЉШєpЃЈxЃЉЁЪMЃЌдђга
ГЩСЂЃЌЫЕУїfЃЈxЃЉЪєгкМЏКЯMЃЎЃЈ2ЃЉШєpЃЈxЃЉЁЪMЃЌдђга![]() ЃЌШЛКѓПЩЧѓГіЕБ
ЃЌШЛКѓПЩЧѓГіЕБ![]() ЪБЃЌpЃЈxЃЉЁЪMЃЎЃЈ3ЃЉжБНгРћгУаТЖЈвхМгвджЄУїЃЌВЂЧѓГіhЃЈxЃЉЕФЁАОјЖдВюЩЯШЗНчЁБTЕФжЕЃЎ
ЪБЃЌpЃЈxЃЉЁЪMЃЎЃЈ3ЃЉжБНгРћгУаТЖЈвхМгвджЄУїЃЌВЂЧѓГіhЃЈxЃЉЕФЁАОјЖдВюЩЯШЗНчЁБTЕФжЕЃЎ
ЃЈ1ЃЉЩш![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
ЁрКЏЪ§![]() ЪєгкМЏКЯ
ЪєгкМЏКЯ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШєКЏЪ§![]() ЃЌ
ЃЌ![]() ЪєгкМЏКЯ
ЪєгкМЏКЯ![]() ЃЌ
ЃЌ
дђЕБ![]() ЪБЃЌ
ЪБЃЌ![]() КуГЩСЂЃЌ
КуГЩСЂЃЌ
МД![]() Жд
Жд![]() КуГЩСЂЃЌ
КуГЩСЂЃЌ
Ёр![]() Жд
Жд![]() КуГЩСЂЃЎ
КуГЩСЂЃЎ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрДцдкЪЕЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌ
ЃЌ![]() ЪєгкМЏКЯ
ЪєгкМЏКЯ![]() ЃЌЧвЪЕЪ§
ЃЌЧвЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШЁ![]() ЃЌ
ЃЌ
дђЖдЧјМф![]() ЕФШЮвтЛЎЗжЃК
ЕФШЮвтЛЎЗжЃК
![]() ЃЌ
ЃЌ
КЭЪН![]()
![]()
![]()
![]()
![]()
![]() ЃЌ
ЃЌ
ЁрМЏКЯ![]() жаЕФКЏЪ§
жаЕФКЏЪ§![]() ЪЧЁАОјЖдВюгаНчКЏЪ§ЁБЃЌЧв
ЪЧЁАОјЖдВюгаНчКЏЪ§ЁБЃЌЧв![]() ЕФЁАОјЖдВюЩЯШЗНчЁБ
ЕФЁАОјЖдВюЩЯШЗНчЁБ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
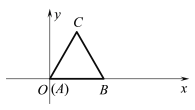
ЁОЬтФПЁПШчЭМЗХжУЕФБпГЄЮЊ2ЕФе§Ш§НЧаЮABCбиxжсЙіЖЏЃЌМЧЙіЖЏЙ§ГЬжаЖЅЕуAЕФКсЁЂзнзјБъЗжБ№ЮЊ![]() КЭ
КЭ![]() ЃЌЧв
ЃЌЧв![]() ЪЧ
ЪЧ![]() дкгГЩф
дкгГЩф![]() зїгУЯТЕФЯѓЃЌдђЯТСаЫЕЗЈжаЃК
зїгУЯТЕФЯѓЃЌдђЯТСаЫЕЗЈжаЃК
Ђй гГЩф![]() ЕФжЕгђЪЧ
ЕФжЕгђЪЧ![]() ЃЛ
ЃЛ
Ђк гГЩф![]() ВЛЪЧвЛИіКЏЪ§ЃЛ
ВЛЪЧвЛИіКЏЪ§ЃЛ
Ђл гГЩф![]() ЪЧКЏЪ§ЃЌЧвЪЧХМКЏЪ§ЃЛ
ЪЧКЏЪ§ЃЌЧвЪЧХМКЏЪ§ЃЛ
Ђм гГЩф![]() ЪЧКЏЪ§ЃЌЧвЕЅдіЧјМфЮЊ
ЪЧКЏЪ§ЃЌЧвЕЅдіЧјМфЮЊ![]() ЃЌ
ЃЌ
Цфжае§ШЗЫЕЗЈЕФађКХЪЧ___________.
ЫЕУїЃКЁАе§Ш§НЧаЮABCбиxжсЙіЖЏЁБАќРЈбиxжсе§ЗНЯђКЭбиxжсИКЗНЯђЙіЖЏЃЎбиxжсе§ЗНЯђЙіЖЏжИЕФЪЧЯШвдЖЅЕуBЮЊжааФЫГЪБеыа§зЊЃЌЕБЖЅЕуCТфдкxжсЩЯЪБЃЌдйвдЖЅЕуCЮЊжааФЫГЪБеыа§зЊЃЌШчДЫМЬајЃЎРрЫЦЕиЃЌе§Ш§НЧаЮABCПЩвдбиxжсИКЗНЯђЙіЖЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЮЊжБНЧЬнаЮЃЌ
ЮЊжБНЧЬнаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧвЦНУц
ЃЌЧвЦНУц![]() ЦНУц
ЦНУц![]() ЃЎ
ЃЎ
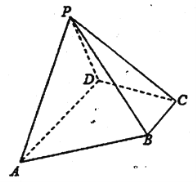
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЯпЖЮ![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙЖўУцНЧ
ЃЌЪЙЖўУцНЧ![]() ЕФДѓаЁЮЊ
ЕФДѓаЁЮЊ![]() ЃЌШєДцдкЃЌЧѓГі
ЃЌШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕЩЯЃЌгавЛЕуСаP0 ЃЌ P1 ЃЌ P2 ЃЌ P3 ЃЌ ЁЃЌPnЉ1 ЃЌ Pn ЃЌ ЩшЕуPkЕФзјБъЃЈxk ЃЌ ykЃЉЃЈkЁЪNЃЌkЁмnЃЉЃЌЦфжаxkЁЂykЁЪZЃЌМЧЁїxk=xkЉxkЉ1 ЃЌ Ёїyk=ykЉykЉ1 ЃЌ ЧвТњзу|Ёїxk||Ёїyk|=2ЃЈkЁЪN* ЃЌ kЁмnЃЉЃЛ
ЃЈ1ЃЉвбжЊЕуP0ЃЈ0ЃЌ1ЃЉЃЌЕуP1ТњзуЁїy1ЃОЁїx1ЃО0ЃЌЧѓP1ЕФзјБъЃЛ
ЃЈ2ЃЉвбжЊЕуP0ЃЈ0ЃЌ1ЃЉЃЌЁїxk=1ЃЈkЁЪN* ЃЌ kЁмnЃЉЃЌЧв{yk}ЃЈkЁЪNЃЌkЁмnЃЉЪЧЕндіЪ§СаЃЌЕуPnдкжБЯпlЃКy=3xЉ8ЩЯЃЌЧѓnЃЛ
ЃЈ3ЃЉШєЕуP0ЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЃЌy2016=100ЃЌЧѓx0+x1+x2+Ё+x2016ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЦНУц![]()
![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЗжБ№ЪЧРтГЄЮЊ1гы2ЕФе§Ш§НЧаЮЃЌ
ЗжБ№ЪЧРтГЄЮЊ1гы2ЕФе§Ш§НЧаЮЃЌ ![]() //
// ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЮЊжБНЧЬнаЮЃЌ
ЮЊжБНЧЬнаЮЃЌ ![]() //
// ![]() ЃЌ
ЃЌ ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжиаФЃЌ
ЕФжиаФЃЌ ![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ ![]() .
.

ЃЈЂёЃЉЕБ![]() ЪБЃЌЧѓжЄЃК
ЪБЃЌЧѓжЄЃК ![]() //ЦНУц
//ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂђЃЉШєжБЯп![]() гы
гы![]() ЫљГЩНЧЮЊ
ЫљГЩНЧЮЊ![]() ЃЌЪдЧѓЖўУцНЧ
ЃЌЪдЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП.КЏЪ§fЃЈxЃЉ=ex+x2+x+1гыgЃЈxЃЉЕФЭМЯѓЙигкжБЯп2xЉyЉ3=0ЖдГЦЃЌPЃЌQЗжБ№ЪЧКЏЪ§fЃЈxЃЉЃЌgЃЈxЃЉЭМЯѓЩЯЕФЖЏЕуЃЌдђ|PQ|ЕФзюаЁжЕЮЊ__
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ ![]() ЗжБ№ЮЊЭждВ
ЗжБ№ЮЊЭждВ![]() ЕФзѓЁЂгвНЙЕуЃЌЭждВРыаФТЪ
ЕФзѓЁЂгвНЙЕуЃЌЭждВРыаФТЪ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЭЈЙ§Еу
ЭЈЙ§Еу![]() ,ЧвЧуаБНЧЪЧ45Ёу.
,ЧвЧуаБНЧЪЧ45Ёу.
(1)ЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
(2)ШєжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФУцЛ§.
ЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌвддЕуЮЊМЋЕуЃЌ ![]() жсЕФе§АыжсЮЊМЋжсЃЌвдЯрЭЌЕФГЄЖШЕЅЮЛНЈСЂМЋзјБъЯЕЃЌвбжЊжБЯп
жсЕФе§АыжсЮЊМЋжсЃЌвдЯрЭЌЕФГЄЖШЕЅЮЛНЈСЂМЋзјБъЯЕЃЌвбжЊжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌЧњЯп
ЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЩш![]() ЮЊВЮЪ§ЃЌШє
ЮЊВЮЪ§ЃЌШє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФВЮЪ§ЗНГЬЃЛ
ЕФВЮЪ§ЗНГЬЃЛ
ЃЈ2ЃЉвбжЊжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() ЃЌЩш
ЃЌЩш![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФзѓгвНЙЕуЗжБ№ЮЊ
ЕФзѓгвНЙЕуЗжБ№ЮЊ![]() ЃЌЩЯЖЅЕуЮЊ
ЃЌЩЯЖЅЕуЮЊ![]() ЃЌШєжБЯп
ЃЌШєжБЯп![]() ЕФаБТЪЮЊ1ЃЌЧвгыЭждВЕФСэвЛИіНЛЕуЮЊ
ЕФаБТЪЮЊ1ЃЌЧвгыЭждВЕФСэвЛИіНЛЕуЮЊ![]() ЃЌ
ЃЌ ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() ЃЈжБЯп
ЃЈжБЯп![]() ЕФаБТЪВЛЮЊ1ЃЉгыЭждВНЛгк
ЕФаБТЪВЛЮЊ1ЃЉгыЭждВНЛгк![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() дкЕу
дкЕу![]() ЕФЩЯЗНЃЌШє
ЕФЩЯЗНЃЌШє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФаБТЪ.
ЕФаБТЪ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com