
【题目】已知矩阵![]() ,
,![]() ,直线
,直线![]() 经矩阵
经矩阵![]() 所对应的变换得到直线
所对应的变换得到直线![]() ,直线
,直线![]() 又经矩阵
又经矩阵![]() 所对应的变换得到直线
所对应的变换得到直线![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】![]()
【解析】
求出![]() ,确定变换前直线
,确定变换前直线![]() 的点与变换后直线
的点与变换后直线![]() 的点坐标关系,利用变换后点在
的点坐标关系,利用变换后点在![]() 上,建立方程,求出
上,建立方程,求出![]() ,同理确定变换前直线
,同理确定变换前直线![]() 的点与变换后直线
的点与变换后直线![]() 的点坐标关系,即可求出结论.
的点坐标关系,即可求出结论.
解:![]()
设P(x,y)是l1上的任意一点,
其在BA所对应的变换作用下的像为(x′,y′),
则![]() ,得
,得![]() ,
,
由题意可得,点(x′,y′)在直线l3上,
所以2ax+by+4=0即为直线l1:x-y+4=0,
故![]() ,b=-1.
,b=-1.
此时![]() ,同理可设Q(x0,y0)为l2上的任意一点,
,同理可设Q(x0,y0)为l2上的任意一点,
其在B所对应的变换作用下的像为(x′0,y′0),
则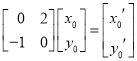 ,得
,得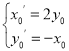 ,
,
又(x′0,y′0)在直线l3上,所以2y0-x0+4=0,
故直线l2的方程为2y-x+4=0,即x-2y-4=0.


科目:高中数学 来源: 题型:
【题目】在边长为![]() 的等边三角形
的等边三角形![]() 中,点
中,点![]() 分别是边
分别是边![]() 上的点,满足
上的点,满足![]() 且
且![]()
![]() ,将
,将![]() 沿直线
沿直线![]() 折到
折到![]() 的位置. 在翻折过程中,下列结论成立的是( )
的位置. 在翻折过程中,下列结论成立的是( )
A.在边![]() 上存在点
上存在点![]() ,使得在翻折过程中,满足
,使得在翻折过程中,满足![]() 平面
平面![]()
B.存在![]() ,使得在翻折过程中的某个位置,满足平面
,使得在翻折过程中的某个位置,满足平面![]() 平面
平面![]()
C.若![]() ,当二面角
,当二面角![]() 为直二面角时,
为直二面角时,![]()
D.在翻折过程中,四棱锥![]() 体积的最大值记为
体积的最大值记为![]() ,
,![]() 的最大值为
的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交抛物线C于A,B两点.
交抛物线C于A,B两点.
(1)求线段AF的中点M的轨迹方程;
(2)已知△AOB的面积是△BOF面积的3倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为厦门市2018年国庆节7天假期的楼房认购量与成交量的折线图,请你根据折线图对这7天的认购量(单位:套)与成交量(单位:套),则下列选项中正确的是( )
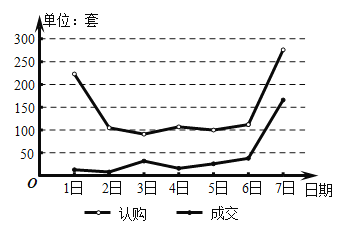
A.日成交量的中位数是10
B.日成交量超过日平均成交量的有2天
C.认购量与日期正相关
D.10月7日认购量的增长率小于10月7日成交量的增长率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医科大学实习小组为研究实习地昼夜温差与患感冒人数之间的关系,分别到当地气象部门和某医院抄录了1月份至3月份每月5日、20日的昼夜温差情况与因患感冒而就诊的人数,得到如表资料:
日期 | 1月5日 | 1月20日 | 2月5日 | 2月20日 | 3月5日 | 3月20日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该小组确定的研究方案是:先从这六组数据中随机选取4组数据求线性回归方程,再用剩余的2组数据进行检验.
(1)求剩余的2组数据中至少有一组是20日的概率;
(2)若选取的是1月20日,2月5日,2月20日,3月5日四组数据.
①请根据这四组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 用分数表示);
用分数表示);
②若由线性回归方程得到的估计数据与剩余的检验数据的误差均不超过1人,则认为得到的线性回归方程是理想的,试问①中所得线性回归方程是否理想?
附参考公式: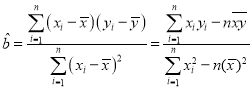 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 平面ABCD,底面ABCD是等腰梯形,
平面ABCD,底面ABCD是等腰梯形,![]() ,
,![]() .
.
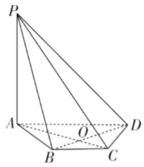
(1)证明:![]() 平面PAC;
平面PAC;
(2)若![]() ,
,![]() ,设
,设![]() ,且
,且![]() ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() (常数
(常数![]() ),
),![]() ,(
,(![]() ,
,![]() ).数列
).数列![]() 满足:
满足:![]()
![]() .
.
(1)分别求![]() ,
,![]() ,
,![]() 的值:
的值:
(2)求数列![]() 的通项公式;
的通项公式;
(3)问:数列![]() 的每一项能否均为整数?若能,求出
的每一项能否均为整数?若能,求出![]() 的所有可能值;若不能,请说明理由.
的所有可能值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com