C
分析:等差数列{a
n}中,由a
1=1,a
7=4,解得d=

.所以
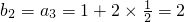
,b
3=b
1q
2=
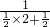
=

,
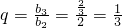
,b
1=6.所以
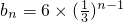
,由
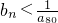
=
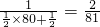
,得
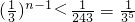
,由此能求出最小正整数n.
解答:等差数列{a
n}中,
∵a
1=1,a
7=4,
∴1+6d=4,
解得d=

.
∴
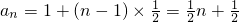
,
∴
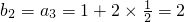
,
b
3=b
1q
2=
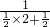
=

,
∴
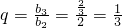
,
∵
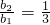
,
∴b
1=6.
∴
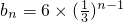
,
∵
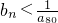
=
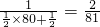
,
∴
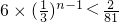
,
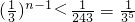
,
∴n-1>5,
∴n>6.
∴最小正整数n是7.
故选C.
点评:本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.

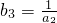 ,则满足
,则满足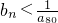 的最小正整数n是
的最小正整数n是