

 ,则甲、乙两用户共应交费1.8×8m≤9.6元,不合题意;
,则甲、乙两用户共应交费1.8×8m≤9.6元,不合题意; <m≤
<m≤ ,则甲、乙两用户共应交费7.2+3(5m-4)+1.8×3m=20.4m-4.8≤22.4,不合题意;
,则甲、乙两用户共应交费7.2+3(5m-4)+1.8×3m=20.4m-4.8≤22.4,不合题意; ,则甲、乙两用户共应交费7.2+3(8m-8)=26.4
,则甲、乙两用户共应交费7.2+3(8m-8)=26.4 ,
, <m≤
<m≤ 和m>
和m> 时用户所交消费,结合甲、乙两用户共交水费26.4元,解方程可得答案.
时用户所交消费,结合甲、乙两用户共交水费26.4元,解方程可得答案.

 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
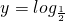 (x+b)的图象(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到3μg/m3,以后逐步减小.
(x+b)的图象(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到3μg/m3,以后逐步减小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
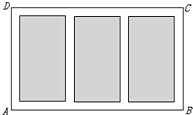 如图,某农业研究所要在一个矩形试验田ABCD内种植三种农作物,三种农作物分别种植在并排排列的三个形状相同、大小相等的矩形中.试验田四周和三个种植区域之间设有1米宽的非种植区.已知种植区的占地面积为800平方米,问:应怎样设计试验田ABCD的长与宽,才能使其占地面积最小?最小占地面积是多少?
如图,某农业研究所要在一个矩形试验田ABCD内种植三种农作物,三种农作物分别种植在并排排列的三个形状相同、大小相等的矩形中.试验田四周和三个种植区域之间设有1米宽的非种植区.已知种植区的占地面积为800平方米,问:应怎样设计试验田ABCD的长与宽,才能使其占地面积最小?最小占地面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:单选题
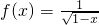 定义域为M,g(x)=lnx定义域为N,则M∩N=
定义域为M,g(x)=lnx定义域为N,则M∩N=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com