练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若点P(x，y)在曲线(θ为参数)上，则使x2＋y2取最大值的点P的坐标是

    [　　]

    A．(6，－8)

    B．(－6，8)

    C．(3，－4)

    D．(－3，4)

    答案：A
    解析：

    曲线是以点(3，－4)为圆心，以5为半径的圆，而x2＋y2表示此圆上的点到原点距离的平方．因圆心到原点距离是5，故此圆恰过原点，而圆上点P(6，－8)到原点的距离的平方最大．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•临沂二模）已知Ω={（x，y）|0≤x≤1，0≤y≤1}，A是由直线y=0，x=a（0＜a≤1）和曲线y=x3围成的曲边三角形的平面区域，若向区域Ω上随机投一点P，点P落在区域A内的概率是
    1
    64
    ，则a的值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•湖南）函数f（x）=sin （ωx+φ）的导函数y=f′（x）的部分图象如图所示，其中，P为图象与y轴的交点，A，C为图象与x轴的两个交点，B为图象的最低点．
    （1）若φ=
    π
    6
    ，点P的坐标为（0，
    3
    		3
    2
    ），则ω=
    3
    3
    ；
    （2）若在曲线段
    ABC
    与x轴所围成的区域内随机取一点，则该点在△ABC内的概率为
    π
    4
    π
    4
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，成都市准备在南湖的一侧修建一条直路EF，另一侧修建一条观光大道，大道的前一部分为曲线段FBC，该曲线段是函数y=Asin(ωx+
    2π3
    )，(A＞0，ω＞0)，x∈[-4，0]    时的图象，且图象的最高点为B（-1，3），大道的中间部分为长1.5km的直线段CD，且CD∥EF．大道的后一部分是以O为圆心的一段圆弧DE．
    （1）求曲线段FBC的解析式，并求∠DOE的大小；
    （2）若南湖管理处要在圆弧大道所对应的扇形DOE区域内修建如图所示的水上乐园PQMN，问点P落在圆弧DE上何处时，水上乐园的面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•深圳二模）已知Ω={（x，y）|0≤x≤1，0≤y≤1}，A是由直线x=1，y=0和曲线y=x3围成的曲边三角形的平面区域，若向区域Ω上随机投一点P，则点P落在区域A内的概率为（　　）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省高三上学期期中考练习二理科数学试卷（解析版） 题型：填空题

    函数f（x）="sin" (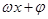)的导函数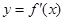的部分图像如图所示，其中，P为图像与y轴的交点，A，C为图像与x轴的两个交点，B为图像的最低点．

    （1）若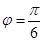，点P的坐标为（0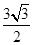，），则      ；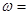

    （2）若在曲线段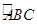与x轴所围成的区域内随机取一点，则该点在△ABC内的概率为      ．

     

    查看答案和解析>>

    同步练习册答案