给出下列命题:
①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②命题“若am2<bm2,则a<b”的逆命题是真命题;
③f(x)是(-∞,0)∪(0,+∞)上的奇函数,x>0时的解析式是f(x)=2*.则x<0时的解析式为f(x)=-2-x;
④若随机变量ξ~N(1,σ2),且P(0≤ξ≤1)=0.3,则P(ξ≥2)=0.2.
其中真命题的序号是 .(写出所有你认为正确命题的序号)
【答案】分析:①所给的命题是一个特称命题,特称命题的否定是全称命题,依据规则写出结论即可,得到①正确;
②通过举反例判断出②不正确;
③设x<0,则-x>0,利用函数是奇函数,结合已知的解析式,即可得到结论;
④利用正态分布曲线的对称性,即可得到结论.
解答:解:对于①,它是一个含有量词的命题,“?x∈R,x2-x>0”即“存在x∈R,使得x2-x>0成立”,其否定应该是不存在满足条件的x,也就是说,对于任意的x∈R,都有x2-x≤0,即“?x∈R,x2-x≤0”,故①正确;
对于②,“若am2<bm2,则a<b”的逆命题为“若a<b,则am2<bm2,当m=0时不成立,故为假命题,即②不正确;
对于③,设x<0,则-x>0,∴f(-x)=2-x,∵函数是(-∞,0)∪(0,+∞)上的奇函数,∴f(x)=-f(x)=-2-x,即③正确;
对于④若随机变量ξ~N(1,σ2),且P(0≤ξ≤1)=0.3,则P(ξ≥2)=P(ξ≤0)=1-0.3=0.2,即④正确.
故答案为:①③④.
点评:本题考查命题的否定、全称命题、考查利用函数的奇偶性求函数的解析式,考查正态分布曲线的对称性,属于中档题.



 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案 y =
y = 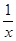 的一个交点;
的一个交点; 的一个交点
的一个交点 的一个交点
的一个交点 (
( 是正整数)为:
是正整数)为:  的一个交点;
的一个交点; 的一个交点;
的一个交点; 的一个交点;
的一个交点; (
( 是正整数)为:
.
是正整数)为:
.