【题目】如图，在平行四边形ABCD中，P，Q分别是BC和CD的中点．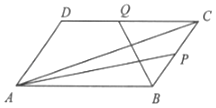 
（1）若AB=2，AD=1，∠BAD=60°，求 
及cos∠BAC的余弦值；
（2）若 
=λ 
+ 
，求λ+μ的值．
【答案】
（1）解：∵平行四边形ABCD中，AB=2，AD=1，∠BAD=60°，
∴ 
= 
（ + 
）= 2+ =22+2×1×cos60°=5，
| 
|2= 2=（ + ）2= 2+2 + 2=22+2×2×1×cos60°+1=7，
∴| |= 
，
cos∠BAC=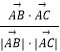 
= 
= 
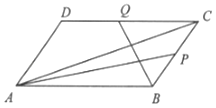
（2）解：∵P，Q分别是BC和CD的中点．
∴ 
= + 
， 
= ﹣ ，
∵ =λ + 
，
∴ + =λ（ + ）+μ（ ﹣ ），
∴ 
，
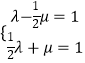解得： 
，
∴λ+μ= 
【解析】（1）由已知中AB=2，AD=1，∠BAD=60°，代入向量数量积公式，可得 ，求出| |，代入cos∠BAC= 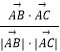可得cos∠BAC的余弦值；（2）若 =λ + ，则 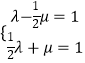，解得答案．
科目：高中数学 来源： 题型：
【题目】已知集合
为集合
的
个非空子集，这
个集合满足：①从中任取
个集合都有
成立；②从中任取
个集合都有
成立．
（Ⅰ）若
， 
， 
，写出满足题意的一组集合
；
（Ⅱ）若
， 
，写出满足题意的一组集合
以及集合
；
（Ⅲ) 若
， 
，求集合
中的元素个数的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在R上函数f（x），且f（x）+f（﹣x）=0，当x＜0时，f（x）=（ 
）x﹣8×（ 
）x﹣1
（1）求f（x）的解析式；
（2）当x∈[1，3]时，求f（x）的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）是定义在R上的偶函数，当x≥0时，f（x）=ax（a＞1），
（1）求函数f（x）的解析式；
（2）若不等式f（x）≤4的解集为[﹣2，2]，求a的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a∈R，函数f（x）=x2﹣2ax+5．
（1）若a＞1，且函数f（x）的定义域和值域均为[1，a]，求实数a的值；
（2）若不等式x|f（x）﹣x2|≤1对x∈[ 
， 
]恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且三角形的面积为S= 
bccosA．
（1）求角A的大小；
（2）若c=8，点D在AC边上，且CD=2，cos∠ADB=﹣ 
，求a的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知实数λ＞0，设函数f（x）=eλx﹣x．
（Ⅰ）当λ=1时，求函数f（x）的极值；
（Ⅱ）若对任意x∈（0，+∞），不等式f（x）≥0恒成立，求λ的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
