
【题目】已知a∈R,函数f(x)=x2﹣2ax+5.
(1)若a>1,且函数f(x)的定义域和值域均为[1,a],求实数a的值;
(2)若不等式x|f(x)﹣x2|≤1对x∈[ ![]() ,
, ![]() ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围.
【答案】
(1)解:∵f(x)的图象开口向上,对称轴为x=a>1,
∴f(x)在[1,a]上单调递减,
∴f(1)=a,即6﹣2a=a,解得a=2
(2)解:不等式x|f(x)﹣x2|≤1对x∈[ ![]() ,
, ![]() ]恒成立,
]恒成立,
即x|2ax﹣5|≤1对x∈[ ![]() ,
, ![]() ]恒成立,
]恒成立,
故a≥ ![]() 且a≤
且a≤ ![]() 在x∈[
在x∈[ ![]() ,
, ![]() ]恒成立,
]恒成立,
令g(x)= ![]() ,x∈[
,x∈[ ![]() ,
, ![]() ],则g′(x)=﹣
],则g′(x)=﹣ ![]() ,
,
令g′(x)>0,解得: ![]() ≤x<
≤x< ![]() ,令g′(x)<0,解得:
,令g′(x)<0,解得: ![]() <x≤
<x≤ ![]() ,
,
故g(x)在[ ![]() ,
, ![]() )递增,在(
)递增,在( ![]() ,
, ![]() ]递减,
]递减,
故g(x)max=g( ![]() )=
)= ![]() ,
,
令h(x)= ![]() ,x∈[
,x∈[ ![]() ,
, ![]() ],h′(x)=
],h′(x)= ![]() <0,
<0,
故h(x)在x∈[ ![]() ,
, ![]() ]递减,
]递减,
h(x)min=h( ![]() )=7,
)=7,
综上: ![]() ≤a≤7.
≤a≤7.
【解析】(1)判断出f(x)的单调性,利用单调性列方程解出;(2)问题转化为a≥ ![]() 且a≤
且a≤ ![]() 在x∈[
在x∈[ ![]() ,
, ![]() ]恒成立,根据函数的单调性求出a的范围即可.
]恒成立,根据函数的单调性求出a的范围即可.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x+
(x+ ![]() ),g(x)=
),g(x)= ![]() (x﹣
(x﹣ ![]() ).
).
(1)求函数h(x)=f(x)+2g(x)的零点;
(2)求函数F(x)=[f(x)]2n﹣[g(x)]2n(n∈N*)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a. 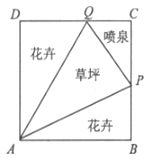
(1)当∠PAQ= ![]() 时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
时,求花卉种植面积S关于a的函数表达式,并求S的最小值;
(2)考虑到小区道路的整体规划,要求PB+DQ=PQ,请探究∠PAQ是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P,Q分别是BC和CD的中点. 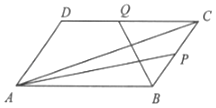
(1)若AB=2,AD=1,∠BAD=60°,求 ![]() 及cos∠BAC的余弦值;
及cos∠BAC的余弦值;
(2)若 ![]() =λ
=λ ![]() +
+ ![]() ,求λ+μ的值.
,求λ+μ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲正弦函数shx= ![]() 和双曲余弦函数chx=
和双曲余弦函数chx= ![]() 与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正弦函数和余弦函数的和角公式,写出双曲正弦或双曲余弦函数的一个类似的正确结论 .
与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正弦函数和余弦函数的和角公式,写出双曲正弦或双曲余弦函数的一个类似的正确结论 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com