
已知向量a= ,b=
,b=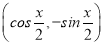 ,且x∈
,且x∈ .
.
(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值为- ,求正实数λ的值.
,求正实数λ的值.
(1)|a+b|=2cosx(2)λ=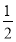
【解析】(1)a·b=cos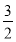 x·cos
x·cos -sin
-sin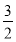 x·sin
x·sin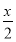 =cos 2x.
=cos 2x.
∵a+b=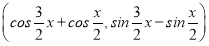 ,
,
∴|a+b|2=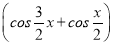 2+
2+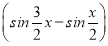 2
2
=2+2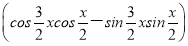 =2+2cos 2x=4cos2x.
=2+2cos 2x=4cos2x.
∵x∈ ,∴cos x≥0.因此|a+b|=2cos x.
,∴cos x≥0.因此|a+b|=2cos x.
(2)由(1)知f(x)=cos 2x-4λcos x=2cos2x-4λcos x-1,
∴f(x)=2(cos x-λ)2-1-2λ2,cos x∈[0,1].
①当0<λ≤1时,当cos x=λ时,
f(x)有最小值-1-2λ2=- ,解得λ=
,解得λ=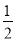 .
.
②当λ>1时,当cos x=1时,f(x)有最小值1-4λ=-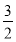 ,
,
λ= (舍去),综上可得λ=
(舍去),综上可得λ=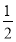


科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评5练习卷(解析版) 题型:填空题
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评3练习卷(解析版) 题型:选择题
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知8b=5c,C=2B,则cos C=( ).
A.  B.-
B.-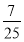 C.±
C.±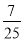 D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评2练习卷(解析版) 题型:选择题
设点P在曲线y=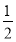 ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
A.1-ln 2 B. (1-ln 2) C.1+ln 2 D.
(1-ln 2) C.1+ln 2 D.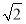 (1+ln 2)
(1+ln 2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评2练习卷(解析版) 题型:选择题
下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( ).
A.y=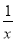 B.y=e-x C.y=-x2+1 D.y=lg |x|
B.y=e-x C.y=-x2+1 D.y=lg |x|
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评1练习卷(解析版) 题型:填空题
设e1,e2为单位向量,且e1,e2的夹角为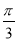 ,若a=e1+3e2,b=2e1,则向量a在b方向上的射影为________.
,若a=e1+3e2,b=2e1,则向量a在b方向上的射影为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题能力测评1练习卷(解析版) 题型:选择题
命题“对任意x∈R,都有x2≥0”的否定为 ( ).
A.对任意x∈R,都有x2<0
B.不存在x∈R,都有x2<0
C.存在x0∈R,使得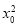 ≥0
≥0
D.存在x0∈R,使得 <0
<0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练8练习卷(解析版) 题型:填空题
在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,P是腰DC上的动点,则|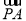 +3
+3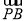 |的最小值为______.
|的最小值为______.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:解答题
已知椭圆的焦点坐标为F1(-1,0),F2(1,0),过F2垂直于长轴的直线交椭圆于P,Q两点,且|PQ|=3.
(1)求椭圆的方程;
(2)过F2的直线l与椭圆交于不同的两点M,N,则△F1MN的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com