
【题目】设函数f(x)=ax+![]() (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
程为y=3.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值,
并求出此定值.
科目:高中数学 来源: 题型:
【题目】2017年5月,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.乘坐高铁可以网络购票,为了研究网络购票人群的年龄分布情况,在5月31日重庆到成都高铁9600名网络购票的乘客中随机抽取了120人进行了统计并记录,按年龄段将数据分成6组:![]() ,得到如图所示的直方图:
,得到如图所示的直方图:
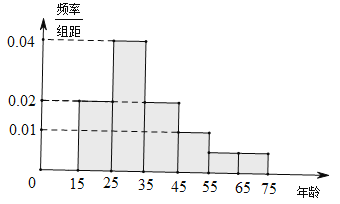
(1)若从总体的9600名网络购票乘客中随机抽取一人,估计其年龄大于35岁的概率;
(2)试估计总体中年龄在区间![]() 内的人数;
内的人数;
(3)试通过直方图,估计5月31日当天网络购票的9600名乘客年龄的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄金分割比例![]() 具有严格的比例性,艺术性,和谐性,蕴含着丰富的美学价值.这一比值能够引起人们的美感,被称为是建筑和艺术中最理想的比例.我们把离心率
具有严格的比例性,艺术性,和谐性,蕴含着丰富的美学价值.这一比值能够引起人们的美感,被称为是建筑和艺术中最理想的比例.我们把离心率![]() 的椭圆称为“黄金椭圆”,则以下四种说法中正确的个数为( )
的椭圆称为“黄金椭圆”,则以下四种说法中正确的个数为( )
①椭圆![]() 是“黄金椭圆;
是“黄金椭圆;
②若椭圆![]() ,
,![]() 的右焦点
的右焦点![]() 且满足
且满足![]() ,则该椭圆为“黄金椭圆”;
,则该椭圆为“黄金椭圆”;
③设椭圆![]() ,
,![]() 的左焦点为F,上顶点为B,右顶点为A,若
的左焦点为F,上顶点为B,右顶点为A,若![]() ,则该椭圆为“黄金椭圆”;
,则该椭圆为“黄金椭圆”;
④设椭圆,![]() ,
,![]() 的左右顶点分别A,B,左右焦点分别是
的左右顶点分别A,B,左右焦点分别是![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() 成等比数列,则该椭圆为“黄金椭圆”;
成等比数列,则该椭圆为“黄金椭圆”;
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆与抛物线![]() 有一个相同的焦点,且该椭圆的离心率为
有一个相同的焦点,且该椭圆的离心率为![]() ,
,
(Ⅰ)求该椭圆的标准方程:
(Ⅱ)求过点![]() 的直线与该椭圆交于A,B两点,O为坐标原点,若
的直线与该椭圆交于A,B两点,O为坐标原点,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选)已知函数![]() ,其中正确结论的是( )
,其中正确结论的是( )
A.当![]() 时,函数
时,函数![]() 有最大值.
有最大值.
B.对于任意的![]() ,函数
,函数![]() 一定存在最小值.
一定存在最小值.
C.对于任意的![]() ,函数
,函数![]() 是
是![]() 上的增函数.
上的增函数.
D.对于任意的![]() ,都有函数
,都有函数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() 是正三角形,
是正三角形,![]() 为
为![]() 的中点,平面
的中点,平面![]() 平面
平面![]() .
.
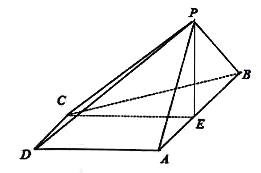
(1)求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com