
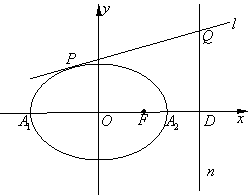
如图,已知椭圆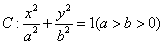 的离心率是
的离心率是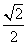 ,
,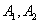 分别是椭圆
分别是椭圆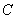 的左、右两个顶点,点
的左、右两个顶点,点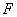 是椭圆
是椭圆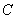 的右焦点。点
的右焦点。点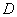 是
是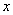 轴上位于
轴上位于 右侧的一点,且满足
右侧的一点,且满足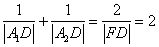 。
。
(1)求椭圆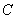 的方程以及点
的方程以及点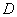 的坐标;
的坐标;
(2)过点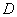 作
作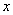 轴的垂线
轴的垂线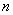 ,再作直线
,再作直线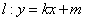 与椭圆
与椭圆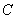 有且仅有一个公共点
有且仅有一个公共点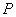 ,直线
,直线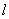 交直线
交直线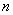 于点
于点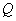 。求证:以线段
。求证:以线段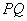 为直径的圆恒过定点,并求出定点的坐标。
为直径的圆恒过定点,并求出定点的坐标。
 |
科目:高中数学 来源: 题型:
甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方有权 向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系x=2000
向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系x=2000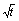 ,若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
,若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
(1)将乙方的年利润W (元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量.
(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量.
(2)甲方每年受乙方生产影响的经济损失余额y=0.002t2.在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格S是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
已知无穷等比数列{an}的各项和为 ,则a1的范围是 ( )
,则a1的范围是 ( )
A.-1<a1<1
B.0<a1<1
c.0<a1< 或
或 <a1<1
<a1<1
D.所给条件不足以确定a1,的范围
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线 的焦点为
的焦点为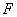 ,顶点为
,顶点为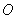 ,准线为
,准线为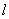 ,过该抛物线上异于顶点
,过该抛物线上异于顶点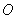 的任意一点
的任意一点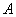 作
作 于点
于点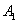 ,以线段
,以线段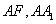 为邻边作平行四边形
为邻边作平行四边形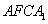 ,连接直线
,连接直线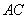 交
交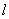 于点
于点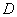 ,延长
,延长 交抛物线于另一点
交抛物线于另一点 。若
。若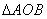 的面积为
的面积为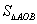 ,
,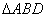 的面积为
的面积为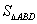 ,则
,则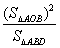 的最大值为____________。
的最大值为____________。
查看答案和解析>>
科目:高中数学 来源: 题型:
一船自西向东匀速航行,上午10时到达一座灯塔P的南偏西75°距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船航行的速度为 ( )
A. 海里/小时 B.
海里/小时 B. 海里/小时
海里/小时
C.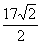 海里/小时 D.
海里/小时 D.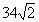 海里/小时
海里/小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com