
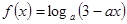
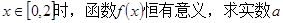 的取值范围;
的取值范围;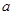 ,使得函数
,使得函数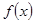 在区间
在区间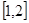 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出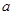 值;若不存在,说明理由。
值;若不存在,说明理由。 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
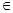 (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
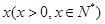 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高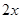 %,而从事蔬菜加工的农民平均每户的年收入将为
%,而从事蔬菜加工的农民平均每户的年收入将为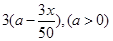 万元.
万元.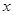 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求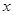 的取值范围;
的取值范围;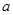 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 10 | m | 5 | 100 |
| B产品 | 20 | 4 | 9 | 60 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
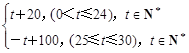 ;该商品的日销售量Q(件)与时间(天)的函数关系式为:
;该商品的日销售量Q(件)与时间(天)的函数关系式为:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
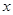 万美元,可获得加工费近似为
万美元,可获得加工费近似为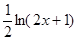 万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失
万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失 万美元,其中
万美元,其中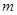 为该时段美元的贬值指数,
为该时段美元的贬值指数,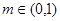 ,从而实际所得的加工费为
,从而实际所得的加工费为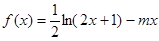 (万美元).
(万美元).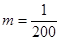 ,为确保企业实际所得加工费随
,为确保企业实际所得加工费随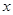 的增加而增加,该企业加工产品订单的金额
的增加而增加,该企业加工产品订单的金额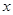 应在什么范围内?
应在什么范围内?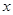 万美元时共需要的生产成本为
万美元时共需要的生产成本为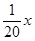 万美元,已知该企业加工生产能力为
万美元,已知该企业加工生产能力为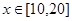 (其中
(其中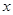 为产品订单的金额),试问美元的贬值指数
为产品订单的金额),试问美元的贬值指数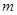 在何范围时,该企业加工生产将不会出现亏损.
在何范围时,该企业加工生产将不会出现亏损.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com