
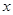 万美元,可获得加工费近似为
万美元,可获得加工费近似为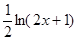 万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失
万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失 万美元,其中
万美元,其中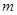 为该时段美元的贬值指数,
为该时段美元的贬值指数,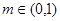 ,从而实际所得的加工费为
,从而实际所得的加工费为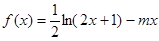 (万美元).
(万美元).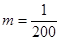 ,为确保企业实际所得加工费随
,为确保企业实际所得加工费随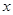 的增加而增加,该企业加工产品订单的金额
的增加而增加,该企业加工产品订单的金额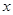 应在什么范围内?
应在什么范围内?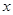 万美元时共需要的生产成本为
万美元时共需要的生产成本为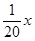 万美元,已知该企业加工生产能力为
万美元,已知该企业加工生产能力为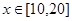 (其中
(其中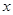 为产品订单的金额),试问美元的贬值指数
为产品订单的金额),试问美元的贬值指数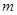 在何范围时,该企业加工生产将不会出现亏损.
在何范围时,该企业加工生产将不会出现亏损.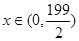 ,该企业实际所得加工费随
,该企业实际所得加工费随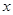 的增加而增加.
的增加而增加.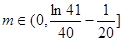 时,该企业加工生产不会亏损.
时,该企业加工生产不会亏损. 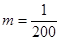 时,
时,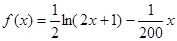 ,然后求导根据导数大于零求得x的取值范围.
,然后求导根据导数大于零求得x的取值范围.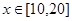 时,都有
时,都有 ,即
,即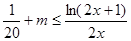 恒成立,然后构造函数
恒成立,然后构造函数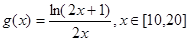 ,利用导数研究它的最小值即可.
,利用导数研究它的最小值即可.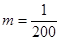 得:
得: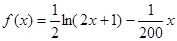 ,其中
,其中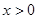
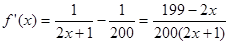 ,由
,由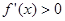 ,即
,即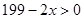 ,
,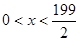
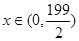 ,该企业实际所得加工费随
,该企业实际所得加工费随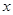 的增加而增加.
的增加而增加.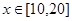 时,都有
时,都有 ,······················· 7分
,······················· 7分 得:
得: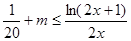
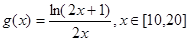 ,则
,则 ·········· 8分
·········· 8分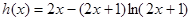 ,则
,则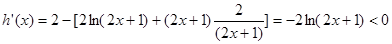 ········ 10分
········ 10分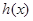 在
在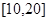 上单调递减,从而
上单调递减,从而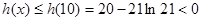 ,··· 11分
,··· 11分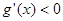 ,可知
,可知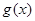 在
在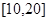 上单调递减,因此
上单调递减,因此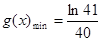 ,即
,即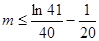 13分
13分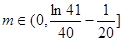 时,该企业加工生产不会亏损. 14分
时,该企业加工生产不会亏损. 14分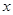 的增加而增加本质就是求函数f(x)的单调增区间.企业加工生产将不会出现亏损本质就是当
的增加而增加本质就是求函数f(x)的单调增区间.企业加工生产将不会出现亏损本质就是当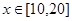 时,不等式
时,不等式 恒成立问题.
恒成立问题.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
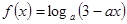
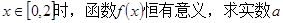 的取值范围;
的取值范围;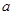 ,使得函数
,使得函数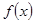 在区间
在区间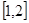 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出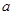 值;若不存在,说明理由。
值;若不存在,说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (月)的函数图象如图所示,则这个工厂对这种产品来说( )
(月)的函数图象如图所示,则这个工厂对这种产品来说( )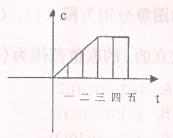
| A.一至三月每月生产数量逐月增加,四、五两月每月生产数量逐月减少 |
| B.一至三月每月生产数量逐月增加,四、五月每月生产数量与三月持平 |
| C.一至三月每月生产数量逐月增加,四、五两月均停止生产 |
| D.一至三月每月生产数量不变,四、五两月均停止生产 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com