
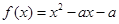 ,
,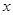 ,使得
,使得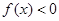 ,求实数
,求实数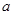 的取值范围;
的取值范围;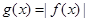 ,且
,且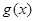 在区间
在区间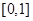 上单调递增,求实数
上单调递增,求实数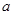 的取值范围。
的取值范围。 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:不详 题型:解答题
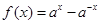 ,
,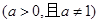 ,
,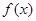 的奇偶性,并证明;
的奇偶性,并证明;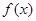 的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)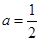 ,方程
,方程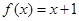 是否有根?如果有根
是否有根?如果有根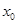 ,请求出一个长度为1的区间
,请求出一个长度为1的区间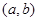 ,使
,使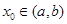 ;如果没有,请说明理由。(注:区间
;如果没有,请说明理由。(注:区间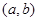 的长度=
的长度=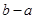 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 10 | m | 5 | 100 |
| B产品 | 20 | 4 | 9 | 60 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
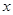 万美元,可获得加工费近似为
万美元,可获得加工费近似为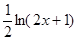 万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失
万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失 万美元,其中
万美元,其中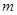 为该时段美元的贬值指数,
为该时段美元的贬值指数,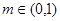 ,从而实际所得的加工费为
,从而实际所得的加工费为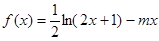 (万美元).
(万美元).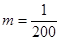 ,为确保企业实际所得加工费随
,为确保企业实际所得加工费随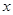 的增加而增加,该企业加工产品订单的金额
的增加而增加,该企业加工产品订单的金额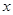 应在什么范围内?
应在什么范围内?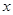 万美元时共需要的生产成本为
万美元时共需要的生产成本为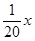 万美元,已知该企业加工生产能力为
万美元,已知该企业加工生产能力为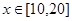 (其中
(其中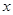 为产品订单的金额),试问美元的贬值指数
为产品订单的金额),试问美元的贬值指数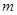 在何范围时,该企业加工生产将不会出现亏损.
在何范围时,该企业加工生产将不会出现亏损.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
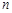 ,定义“
,定义“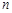
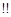 ”如下:当
”如下:当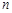 是偶数时,
是偶数时,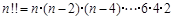 ,
, 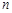 是奇数时,
是奇数时,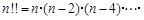
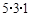 .现在有如下四个命题:
.现在有如下四个命题: 的个位数是0;
的个位数是0; 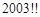 的个位数是5;
的个位数是5;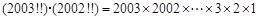 ;
; 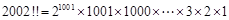 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com