
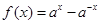 ,
,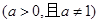 ,
,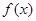 的奇偶性,并证明;
的奇偶性,并证明;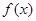 的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)
的单调性,并说明理由。(不需要严格的定义证明,只要说出理由即可)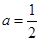 ,方程
,方程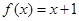 是否有根?如果有根
是否有根?如果有根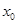 ,请求出一个长度为1的区间
,请求出一个长度为1的区间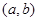 ,使
,使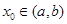 ;如果没有,请说明理由。(注:区间
;如果没有,请说明理由。(注:区间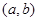 的长度=
的长度=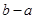 )
)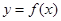 为奇函数,证明:见解析;
为奇函数,证明:见解析;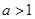 时,
时,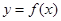 单调递增;
单调递增;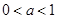 ,
,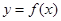 单调递减。
单调递减。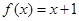 有根
有根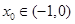 。
。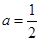 ,
,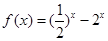 ,又
,又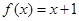 ,再令
,再令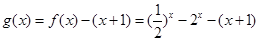 ,
,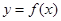 为奇函数……………………1分
为奇函数……………………1分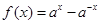 的定义域为R,关于原点对称 …………………2分
的定义域为R,关于原点对称 …………………2分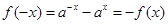 …………………………………………3分
…………………………………………3分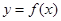 为奇函数……………………………………………4分
为奇函数……………………………………………4分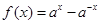 =
=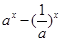
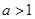 时,
时,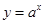 单调递增,
单调递增,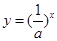 单调递减,
单调递减,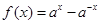 单调递增…………………………………………………6分
单调递增…………………………………………………6分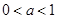 时,
时,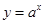 单调递减,
单调递减,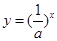 单调递增,
单调递增,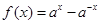 单调递减。
单调递减。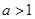 时,
时,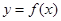 单调递增;
单调递增;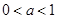 ,
,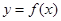 单调递减。
单调递减。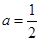 ,
,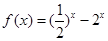 ,又
,又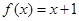
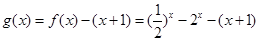 …………………………………9分
…………………………………9分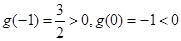 ………………………………………………10分
………………………………………………10分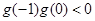 ,故
,故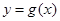 存在零点
存在零点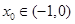
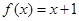 有根
有根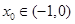 ……………………………………………12分
……………………………………………12分

科目:高中数学 来源:不详 题型:填空题
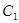 的方程是
的方程是
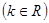 ,曲线
,曲线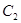 的方程是
的方程是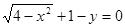 ,给出下列结论:
,给出下列结论: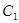 恒过定点
恒过定点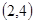 ;
;  ②曲线
②曲线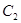 的图形是一个圆;
的图形是一个圆;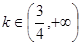 时,
时,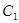 与
与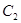 有一个公共点; ④若
有一个公共点; ④若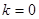 时,则
时,则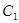 与
与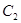 必无公共点。
必无公共点。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
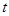 (月)的函数图象如图所示,则这个工厂对这种产品来说( )
(月)的函数图象如图所示,则这个工厂对这种产品来说( )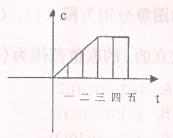
| A.一至三月每月生产数量逐月增加,四、五两月每月生产数量逐月减少 |
| B.一至三月每月生产数量逐月增加,四、五月每月生产数量与三月持平 |
| C.一至三月每月生产数量逐月增加,四、五两月均停止生产 |
| D.一至三月每月生产数量不变,四、五两月均停止生产 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 元(一年定期),若年利率为
元(一年定期),若年利率为 保持不变,且每年到期存款和利息自动转为新的一年定期,到2011年底将所有存款及利息全部取回,则可取回的钱数(元)为
保持不变,且每年到期存款和利息自动转为新的一年定期,到2011年底将所有存款及利息全部取回,则可取回的钱数(元)为A.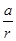 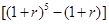 | B.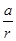 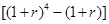 |
C.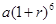 | D.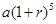 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com