
已知线段PQ两端点的坐标分别为(-1,1)、(2,2),若直线l:x+my+m=0与线段PQ有交点,求m的范围.
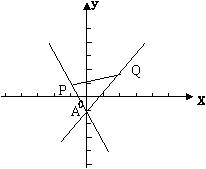 解:(方法一)直线l:x+my+m=0恒过A(0,-1)点,
解:(方法一)直线l:x+my+m=0恒过A(0,-1)点,![]() ,
,![]()
则![]() 或
或![]() ∴
∴![]() 且m≠0
且m≠0
又∵m=0时直线l:x+my+m=0与线段PQ有交点,
∴所求m的范围是![]()
(方法二)∵P,Q两点在直线的两侧或其中一点在直线l上,
∴(-1+m+m)·(2+2 m +m)≤0解得:![]()
∴所求m的范围是![]()
(方法三)设直线l:x+my+m=0与线段PQ有交点为M且M不同于P,Q两点,
设![]() >0)由向量相等得:M
>0)由向量相等得:M![]()
∵直线过点A(0,-1)
∴直线的斜率k=![]() 而
而![]() >0∴
>0∴![]() >0解得:
>0解得:![]() >
>![]() 或
或![]() <-2
<-2
而直线l:x+my+m=0当m≠0时:斜率为![]()
∴![]() >
>![]() 或
或![]() <-2∴
<-2∴![]() <m<
<m<![]()
当M与P重合时,k=-2;当M与P重合时,k=![]()
∴所求m的范围是![]()


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com