
设二次函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:
①当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)成立;
②当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立.
(1)求f(1)的值;
(2)求f(x)的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当x∈[1,m]时,就有f(x+t)≤x成立.
|
解:(1)在②中令x=1,有1≤f(1)≤1,故f(1)=1 3分 (2)由①知二次函数的关于直线x=-1对称,且开口向上 故设此二次函数为f(x)=a(x+1)2,(a>0),∵f(1)=1,∴a= ∴f(x)= (3)假设存在t∈R,只需x∈[1,m],就有f(x+t)≤x. f(x+t)≤x 令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m]. ∴m≤1-t+2 t=-4时,对任意的x∈[1,9] 恒有g(x)≤0,∴m的最大值为9 14分 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:浙江省杭州高中2006-2007学年度第一学期高三年级第三次月考 数学试题(文) 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第26期 总182期 人教课标高一版 题型:044
设二次函数f(x)=x2+2x+b的图象与两坐标轴有三个交点,经过这三个交点的圆记为圆C.
(1)求实数b的取值范围;
(2)求圆C的方程;
(3)问圆C是否经过某定点(其坐标与b无关)?若是,求出定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届云南省高一下学期期末数学试卷(解析版) 题型:解答题
(12分)(1)设x、y、z R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥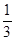 ;
;
(2)设二次函数f (x)=ax2+bx+c (a>0),方程f (x)-x=0有两个实根x1,x2,
且满足:0<x1<x2< ,若x
,若x (0,x1)。
(0,x1)。
求证:x<f (x)<x1
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)当x∈(0,x1)时,证明x<f(x)<x1;
(2)设函数f(x)的图象关于直线x=x0对称;
证明:x0<![]()
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设二次函数f(x)=x2+ax+a,方程f(x)-x=0的两根x1和x2满足0<x1<x2<1.
(1)求实数a的取值范围;
(2)试比较f(0)·f(1)-f(0)与的大小,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com