
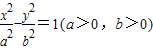 的一条准线被它的两条渐近线截得线段的长度等于它的一个焦点到一条渐近线的距离,则双曲线的两条渐近线的夹角为 .
的一条准线被它的两条渐近线截得线段的长度等于它的一个焦点到一条渐近线的距离,则双曲线的两条渐近线的夹角为 . 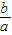 x,准线方程为x=±
x,准线方程为x=±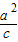
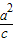 •
•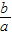 =
=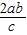
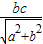 =b
=b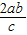 ,整理得2a=c
,整理得2a=c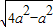 =
=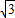 a
a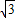 x
x

科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2ab | ||
|
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2ab | ||
|
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市高三三诊模拟考试文科数学 题型:填空题
.已知P是双曲线 的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为
的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为 ,有下列命题:
,有下列命题:
①双曲线的一条准线被它的两条渐近线所截得的线段长度为 ;
;
②若 ;
;
③ 的内切圆的圆心横坐标为
的内切圆的圆心横坐标为 ;
;
④若直线PF1的斜率为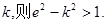
其中正确的命题的序号是 。
查看答案和解析>>
科目:高中数学 来源:2010年四川省高三第三次模拟考试(理) 题型:填空题
已知P是双曲线 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
①双曲线的一条准线被它的两条渐近线所截得的线段长度为
②若 ,则e的最大值为
,则e的最大值为
③ 的内切圆的圆心横坐标为a;
的内切圆的圆心横坐标为a;
④若直线PF1的斜率为k,则
其中正确的命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com