练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知球的表面积为64π，则它的体积为（　　）
    A．16πB．$\frac{256}{3}$πC．36πD．$\frac{100}{3}$π

    分析 根据球的表面积公式求出球的半径，然后计算球的体积即可．

    解答 解：设球的半径为r，
    ∵球的表面积为64π，
    ∴4πr2=64π，即r2=16，
    解得r=4，
    ∴球的体积为$\frac{4}{3}π×{4}^{3}$=$\frac{256}{3}π$．
    故选B．

    点评 本题主要考查球的表面积和体积的计算，要求熟练掌握相应的表面积和体积公式，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．执行如图的程序框图，若输入a=10011，k=2，n=5，则输出的b的值是（　　）
    A．38B．39C．18D．19

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知命题p：“?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是奇函数”，则命题?p为（　　）
    A．?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是偶函数B．?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是奇函数
    C．?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$不是奇函数D．?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$不是奇函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在正方体ABCD-A1B1C1D1中，若AD的中点为M，DD1的中点为N，则异面直线MN与BD所成角的大小是60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

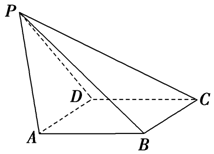    16．如图，已知四棱锥P-ABCD，侧面PAD是正三角形，底面ABCD是菱形，∠BAD=60°，设平面PAD∩平面PBC=l．
    （Ⅰ）求证：l∥平面ABCD；
    （Ⅱ）求证：PB⊥BC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．如图，在直四棱柱（侧棱与底面垂直的四棱柱）ABCD-A1B1C1D1中，已知DC=DD1=2AD=2AB，AD⊥DC，AB∥DC，给出以下结论：
    ①异面直线A1B1与CD1所成的角为45°；
    ②D1C⊥AC1；
    ③在棱DC上存在一点E，使D1E∥平面A1BD，这个点为DC的中点；
    ④在棱AA1上不存在点F，使三棱锥F-BCD的体积为直 四棱柱体积的$\frac{1}{5}$．
    其中正确的有①②③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．如图，等腰梯形ABCD中，AB∥CD，AD⊥BD，矩形ABEF所在的平面和平面ABCD相互垂直． 
    （1）求证：AD⊥平面DBE；
    （2）若AB=2，AD=AF=1，求三棱锥C-BDE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

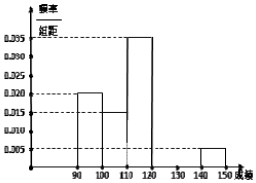    5．某校高三数学竞赛初赛考试结束后，对考生成绩进行统计（考生成绩均不低于90分，满分150分），将成绩按如下方式分为六组，第一组．如图为其频率分布直方图的一部分，若第四、五、六组的人数依次成等差数列，且第六组有4人．
    （1）请补充完整频率分布直方图，并估计这组数据的平均数M；
    （2）现根据初赛成绩从第四组和第六组中任意选2人，记他们的成绩分别为x，y．若|x-y|≥10，则称此二人为“黄金帮扶组”，试求选出的二人为“黄金帮扶组”的概率P1；
    （3）以此样本的频率当作概率，现随机在这组样本中选出3名学生，求成绩不低于120分的人数ξ的分布列及期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知实数a满足下列两个条件：
    ①关于x的方程ax2+3x+1=0有解；
    ②代数式log2（a+3）有意义．
    则使得指数函数y=（3a-2）x为减函数的概率为（　　）
    A．$\frac{4}{63}$B．$\frac{1}{16}$C．$\frac{3}{63}$D．$\frac{3}{16}$

    查看答案和解析>>

    同步练习册答案