-1或-5 |a-b|≥6

分析:(A)把曲线
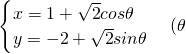
是参数)的参数方程化为普通方程可得表示一个圆,再由直线l:x-y+b=0与曲线相切可得圆心到直线的距离等于半径,由此求得b的值.
(B)由于|x-a|+|x-b|表示数轴上的x对应点到a、b对应点的距离之和,其最小值为|a-b|,可得|a-b|≥6.
(C)由切线性质可知OC垂直于直线l,得出OC平行于AD,根据AB为圆的直径,得到三角形ABC为直角三角形,再根据BC和AB的长度,利用勾股定理求出AC的长,且利用在直角三角形的性质推出∠CAD等于30°,从而求得求出CD.
解答:(A)把曲线
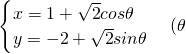
是参数)的参数方程化为普通方程为 (x-1)
2+(y+2)
2=2,表示以A(1,-2)为圆心,半径等于

的圆.
由直线l:x-y+b=0与曲线相切可得

=
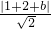
,解得 b=-1 或 b=-5,
故答案为-1或-5.
(B)由于|x-a|+|x-b|表示数轴上的x对应点到a、b对应点的距离之和,其最小值为|a-b|,故由6≤|x-a|+|x-b|对任意的x∈R恒成立,
可得|a-b|≥6,
故答案为|a-b|≥6.
(C)连接OC,则OC⊥直线l,所以OC∥AD.∵AB为圆的直径,∴∠ACB=90°.
又AB=6,BC=3,所以∠CAB=30°,AC=
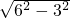
=3

,由OA=OC得,∠ACO=∠CAB=30°.
∵OC∥AD,∴∠CAD=∠ACO=30°,∴CD=
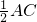
=
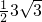
=

,
故答案为

.
点评:本题主要考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,直线和圆的位置关系.绝对值的意义,绝对值不等式的解法.学生灵活运用圆的切线垂直于过切点的直径,掌握圆中的一些基本性质,灵活运用直角三角形的边角关系化简求值,是一道综合题.

 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)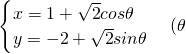 是参数)相切,则b=________.
是参数)相切,则b=________.
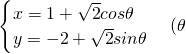 是参数)的参数方程化为普通方程可得表示一个圆,再由直线l:x-y+b=0与曲线相切可得圆心到直线的距离等于半径,由此求得b的值.
是参数)的参数方程化为普通方程可得表示一个圆,再由直线l:x-y+b=0与曲线相切可得圆心到直线的距离等于半径,由此求得b的值.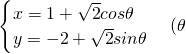 是参数)的参数方程化为普通方程为 (x-1)2+(y+2)2=2,表示以A(1,-2)为圆心,半径等于
是参数)的参数方程化为普通方程为 (x-1)2+(y+2)2=2,表示以A(1,-2)为圆心,半径等于 的圆.
的圆. =
=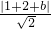 ,解得 b=-1 或 b=-5,
,解得 b=-1 或 b=-5,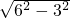 =3
=3 ,由OA=OC得,∠ACO=∠CAB=30°.
,由OA=OC得,∠ACO=∠CAB=30°.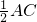 =
=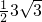 =
= ,
, .
.

 阅读快车系列答案
阅读快车系列答案 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)