
分析 由题意画出集合B所表示的图形,结合A∩B=∅得到a,b所满足的不等式组,由线性规划知识结合补集思想求得2a+3b的取值范围.
解答 解:由题意画出集合B所表示的图形如图,
若A∩B=∅,则$\left\{\begin{array}{l}{b-1>0}\\{2b-1>0}\\{a+b-1>0}\end{array}\right.$或$\left\{\begin{array}{l}{b-1<0}\\{2b-1<0}\\{a+b-1<0}\end{array}\right.$.
令z=2a+3b.
作出可行域如图,
化z=2a+3b为$b=-\frac{2}{3}a+\frac{z}{3}$,
由图可知,当直线$b=-\frac{2}{3}a+\frac{z}{3}$过(0,1)时,z的值为3;
当直线$b=-\frac{2}{3}a+\frac{z}{3}$过($\frac{1}{2},\frac{1}{2}$)时,z的值为$\frac{5}{2}$.
由补集思想可得:若A∩B≠∅恒成立,则2a+3b的取值范围是[$\frac{5}{2},3$].
故答案为:[$\frac{5}{2},3$].
点评 本题考查交集及其运算,考查了数形结合的解题思想方法及数学转化思想方法,难度较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 480 | C. | 216 | D. | 432 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
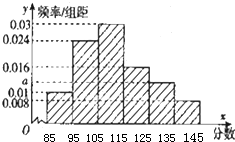 某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (120,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[85,95),第二组[95,105),…第六组[135,145],得到如图所示的频率分布直方图.
某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (120,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[85,95),第二组[95,105),…第六组[135,145],得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com