
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:

(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;
(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
科目:高中数学 来源: 题型:
【题目】袋中有红、白球各一个,每次任取一个,有放回地摸三次,求基本事件的个数n,写出所有基本事件的全集I,并计算下列事件的概率:
(1)三次颜色恰有两次同色;
(2)三次颜色全相同;
(3)三次摸到的红球多于白球.
查看答案和解析>>
科目:高中数学 来源: 题型:
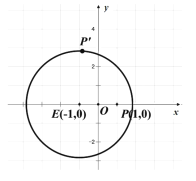
【题目】如图,一张坐标纸上一已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于两个不同的点
交于两个不同的点![]() ,且直线
,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.

(1)自变量![]() 的取值范围是除
的取值范围是除![]() 外的全体实数,
外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出一条函数性质;
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________;
的实数根的情况是________;
②方程![]() 有_______个实数根;
有_______个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学习函数时,我们经历了“确定函数的表达式利用函数图象研究其性质——运用函数解决问题“的学习过程,在画函数图象时,我们通过列表、描点、连线的方法画出了所学的函数图象.同时,我们也学习过绝对值的意义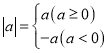 .
.
结合上面经历的学习过程,现在来解决下面的问题:
在函数![]() 中,当
中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中,请直接画出此函数的图象并写出这个函数的两条性质;
(3)在图中作出函数![]() 的图象,结合你所画的函数图象,直接写出不等式
的图象,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.


A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(![]() )(0<a<1,b>0)为奇函数,当x∈(﹣1,a]时,函数y=f(x)的值域是(﹣∞,1].
)(0<a<1,b>0)为奇函数,当x∈(﹣1,a]时,函数y=f(x)的值域是(﹣∞,1].
(1)确定b的值;
(2)证明函数y=f(x)在定义域上单调递增,并求a的值;
(3)若对于任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人投篮命中的概率分别为![]() 与
与![]() ,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
,各自相互独立.现两人做投篮游戏,共比赛3局,每局每人各投一球.
(1)求比赛结束后甲的进球数比乙的进球数多1的概率;
(2)设![]() 表示比赛结束后甲、乙两人进球数的差的绝对值,求
表示比赛结束后甲、乙两人进球数的差的绝对值,求![]() 的概率分布和数学期望
的概率分布和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数.
试问:(1)能组成多少个不同的五位偶数?
(2)五位数中,两个偶数排在一起的有几个?
(3)两个偶数不相邻且三个奇数也不相邻的五位数有几个?(所有结果均用数值表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com