
【题目】从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数.
试问:(1)能组成多少个不同的五位偶数?
(2)五位数中,两个偶数排在一起的有几个?
(3)两个偶数不相邻且三个奇数也不相邻的五位数有几个?(所有结果均用数值表示)
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:

(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;
(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.

给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰坦尼克号》中一暮暮感人画面,让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济,更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型![]() 比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市
比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
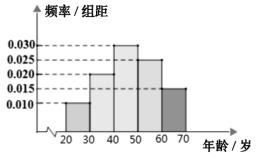
(1)求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄在
人,求所抽取的人中恰好没有年龄在![]() 段的概率.
段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一个关于平面图形的命题:如图,同一平面内有两个边长都是2的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为______.
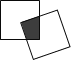
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从标准质量为500g的一批洗衣粉中,随机抽查了50袋,测得的质量数据如下(单位:g):
494 498 493 494 496 492 490 490 500 499 494 495 482 485 502
493 505 485 501 491 493 500 509 512 484 509 510 494 497 498
504 498 483 510 503 497 502 498 497 500 493 499 505 493 491
497 515 503 498 518
(1)找出这组数的最值,求出极差;
(2)以![]() 为第一个分组的区间,作出这组数的频率分布表.
为第一个分组的区间,作出这组数的频率分布表.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 的方程化为普通方程,将
的方程化为普通方程,将![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数,且
为参数,且![]() ),
),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
已知抛物线![]() 的焦点F与椭圆
的焦点F与椭圆![]() 的一个焦点重合,点
的一个焦点重合,点![]() 在抛物线上,过焦点F的直线l交抛物线于A,B两点.
在抛物线上,过焦点F的直线l交抛物线于A,B两点.
(1)求抛物线C的标准方程以及![]() 的值.
的值.
(2)记抛物线的准线![]() 轴交于点H,试问是否存在常数
轴交于点H,试问是否存在常数![]() ,使得
,使得![]() ,且
,且![]() 都成立.若存在,求出
都成立.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com