
分析 (Ⅰ)求函数的导数,根据函数单调性和导数之间的关系即可求函数f(x)的单调区间;
(Ⅱ)当a=1时,根据函数极值和导数之间的关系即可求函数f(x)的极值;
(Ⅲ)设出切点坐标为(m,amem),求出切线斜率和方程,根据导数的几何意义建立方程关系即可求实数a的值.
解答 解:(Ⅰ)函数的导数f′(x)=a(ex+xex)=a(1+x)ex,
若a>0,由f′(x)>0得x>-1,即函数的单调递增区间为(-1,+∞),
由f′(x)<0,得x<-1,即函数的单调递减区间为(-∞,-1),
若a<0,由f′(x)>0得x<-1,即函数的单调递增区间为(-∞,-1),
由f′(x)<0,得x>-1,即函数的单调递减区间为(-1,+∞);
(Ⅱ)当a=1时,由(1)得函数的单调递增区间为(-1,+∞),函数的单调递减区间为(-∞,-1),
即当x=-1时,函数f(x)取得极大值为f(-1)=-$\frac{1}{e}$,无极小值;
(Ⅲ)设切点为(m,amem),
则对应的切线斜率k=f′(m)=a(1+m)em,
则切线方程为y-amem=a(1+m)em(x-m),
即y=a(1+m)em(x-m)+amem=a(1+m)emx-ma(1+m)em+amem=a(1+m)emx-m2aem,
∵y=e(x-$\frac{1}{2}$)=y=ex-$\frac{1}{2}$e,
∴$\left\{\begin{array}{l}{a(1+m){e}^{m}=e}\\{a{m}^{2}{e}^{m}=\frac{1}{2}e}\end{array}\right.$
∴$\left\{\begin{array}{l}{m=1}\\{a=\frac{1}{2}}\end{array}\right.$,
即若直线y=e(x-$\frac{1}{2}$)是曲线y=f(x)的切线,则实数a的值是$\frac{1}{2}$.
点评 本题主要考查导数的应用以及导数的几何意义,求函数的导数,利用函数单调性和导数之间的关系是解决本题的关键.注意要对a进行分类讨论,综合性较强,运算量较大.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知p:?a∈R,方程ax2-2x+a=0有正实数,则¬p:?a∈R,方程ax2-2x+a=0有负实根 | |
| B. | 若X~N(3,4),则P(X<1-3a)=P(X>a2+7)成立的一个必要不充分条件是a=2 | |
| C. | 若函数f(x)=-$\frac{1}{3}$x3+2x2-mx-1在R上是减函数,则m>4 | |
| D. | 若y与x的相关系数r=1,则y与x有线性相关关系,且正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 合计 | |
| 男性 | 16 | 14 | 30 |
| 女性 | 44 | 26 | 70 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,3) | B. | {1,2,3} | C. | {1,2} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
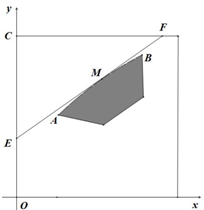 如图,某城市有一个边长为4百米的正方形休闲广场,广场中间阴影部分是一个雕塑群.建立坐标系(单位:百米),则雕塑群的左上方边缘曲线AB是抛物线y2=4x(1≤x≤3,y≥0)的一段.为方便市民,拟建造一条穿越广场的直路EF(宽度不计),要求直路EF与曲线AB相切(记切点为M),并且将广场分割成两部分,其中直路EF左上部分建设为主题陈列区.记M点到OC的距离为m(百米),主题陈列区的面积为S(万平方米).
如图,某城市有一个边长为4百米的正方形休闲广场,广场中间阴影部分是一个雕塑群.建立坐标系(单位:百米),则雕塑群的左上方边缘曲线AB是抛物线y2=4x(1≤x≤3,y≥0)的一段.为方便市民,拟建造一条穿越广场的直路EF(宽度不计),要求直路EF与曲线AB相切(记切点为M),并且将广场分割成两部分,其中直路EF左上部分建设为主题陈列区.记M点到OC的距离为m(百米),主题陈列区的面积为S(万平方米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com