
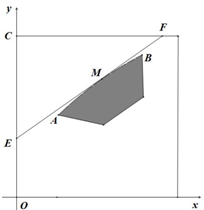
 ��ͼ��ij������һ���߳�Ϊ4�������������й㳡���㳡�м���Ӱ������һ������Ⱥ����������ϵ����λ�����ף��������Ⱥ�����Ϸ���Ե����AB��������y2=4x��1��x��3��y��0����һ�Σ�Ϊ���������⽨��һ����Խ�㳡��ֱ·EF�����Ȳ��ƣ���Ҫ��ֱ·EF������AB���У����е�ΪM�������ҽ��㳡�ָ�������֣�����ֱ·EF���ϲ��ֽ���Ϊ�������������M�㵽OC�ľ���Ϊm�����ף�����������������ΪS����ƽ���ף���
��ͼ��ij������һ���߳�Ϊ4�������������й㳡���㳡�м���Ӱ������һ������Ⱥ����������ϵ����λ�����ף��������Ⱥ�����Ϸ���Ե����AB��������y2=4x��1��x��3��y��0����һ�Σ�Ϊ���������⽨��һ����Խ�㳡��ֱ·EF�����Ȳ��ƣ���Ҫ��ֱ·EF������AB���У����е�ΪM�������ҽ��㳡�ָ�������֣�����ֱ·EF���ϲ��ֽ���Ϊ�������������M�㵽OC�ľ���Ϊm�����ף�����������������ΪS����ƽ���ף������� ��1��M��m��2$\sqrt{m}$����${y}^{'}=\frac{1}{\sqrt{x}}$�����߷���Ϊy-2$\sqrt{m}$=$\frac{1}{\sqrt{m}}$��x-m�����Ӷ������E��0��$\frac{4}{3}$����F��$\frac{32}{9}$��4�����ɴ��������MΪEF�е�ʱ��S��ֵ��
��2����E��0��$\sqrt{m}$����F��4$\sqrt{m}$-m��4����ֱ·EF���ϲ���Ϊ��CEF��S=$\frac{1}{2}��m\sqrt{m}-8m+16\sqrt{m}��$��1��m��3����t=$\sqrt{m}$����S=f��t��=$\frac{1}{2}$��t3-8t2+16t����������������õ��������������S��ȡֵ��Χ��
��� �⣺��1����ֱ·EF������AB��y2=4x��1��x��3��y��0�����У����е�ΪM����M�㵽OC�ľ���Ϊm�����ף���
��M������ΪM��m��2$\sqrt{m}$����
����AB����Ϊy=2$\sqrt{x}$����1��x��3����
��${y}^{'}=\frac{1}{\sqrt{x}}$�����߷���Ϊy-2$\sqrt{m}$=$\frac{1}{\sqrt{m}}$��x-m����
���E��0��$\sqrt{m}$����F��4$\sqrt{m}$-m��4����
��MΪEF�е㣬��$\sqrt{m}+4=4\sqrt{m}$����$\sqrt{m}=\frac{4}{3}$��
���E��0��$\frac{4}{3}$����F��$\frac{32}{9}$��4����
��ʱS=$\frac{1}{2}��\frac{32}{9}����4-\frac{4}{3}��$=$\frac{128}{27}$��
��2���ɣ�1��֪��E��0��$\sqrt{m}$����F��4$\sqrt{m}$-m��4����
��${x}_{F}-4=4\sqrt{m}-m-4$=-��$\sqrt{m}-2$��2��0����xF��4��
��${y}_{E}=\sqrt{m}$��0����ֱ·EF���ϲ���Ϊ��CEF��
S=$\frac{1}{2}CF•CE$=$\frac{1}{2}��4\sqrt{m}-m����4-\sqrt{m}��$=$\frac{1}{2}��m\sqrt{m}-8m+16\sqrt{m}��$��1��m��3��
��t=$\sqrt{m}$����1$��t��\sqrt{3}$����S=f��t��=$\frac{1}{2}$��t3-8t2+16t����
${f}^{'}��t��=\frac{1}{2}��3{t}^{2}-16t+16��=\frac{1}{2}��3t-4����t-4��$��
��1$��t��\frac{4}{3}$ʱ��f�䣨t����0����$\frac{4}{3}��t��\sqrt{3}$ʱ��f�䣨t����0��
��${S}_{max}=f��t��_{max}=f��\frac{4}{3}��=\frac{128}{27}$��
��f��$\sqrt{3}$��=$\frac{19\sqrt{3}-24}{2}$��f��1��=$\frac{9}{2}$��
��S��ȡֵ��ΧΪ��$\frac{19\sqrt{3}-24}{2}$��$\frac{128}{27}$]��
���� ���⿼�������ȡֵ��Χ�������е��⣬����ʱҪ�������⣬ע�����������ʡ������ļ������塢��Ԫ�����������ʵĺ������ã�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 1 | D�� | log23 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com