
分析 (2x2-$\frac{1}{x}}$)6的展开式的通项公式:Tr+1=(-1)r26-r${∁}_{6}^{r}$x12-3r,分别令12-3r=-1,0,解得r,即可得出.
解答 解:(2x2-$\frac{1}{x}}$)6的展开式的通项公式:Tr+1=${∁}_{6}^{r}$(2x2)6-r$(-\frac{1}{x})^{r}$=(-1)r26-r${∁}_{6}^{r}$x12-3r,
分别令12-3r=-1,0,解得r=$\frac{13}{3}$,4.
取r=4,∴(x+1)(2x2-$\frac{1}{x}}$)6的展开式的常数项为1×${2}^{2}{∁}_{6}^{4}$=60.
故答案为:60.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,3) | B. | {1,2,3} | C. | {1,2} | D. | {2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
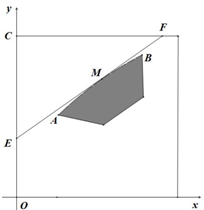 如图,某城市有一个边长为4百米的正方形休闲广场,广场中间阴影部分是一个雕塑群.建立坐标系(单位:百米),则雕塑群的左上方边缘曲线AB是抛物线y2=4x(1≤x≤3,y≥0)的一段.为方便市民,拟建造一条穿越广场的直路EF(宽度不计),要求直路EF与曲线AB相切(记切点为M),并且将广场分割成两部分,其中直路EF左上部分建设为主题陈列区.记M点到OC的距离为m(百米),主题陈列区的面积为S(万平方米).
如图,某城市有一个边长为4百米的正方形休闲广场,广场中间阴影部分是一个雕塑群.建立坐标系(单位:百米),则雕塑群的左上方边缘曲线AB是抛物线y2=4x(1≤x≤3,y≥0)的一段.为方便市民,拟建造一条穿越广场的直路EF(宽度不计),要求直路EF与曲线AB相切(记切点为M),并且将广场分割成两部分,其中直路EF左上部分建设为主题陈列区.记M点到OC的距离为m(百米),主题陈列区的面积为S(万平方米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com