
分析 分别求出关于p,q成立的m的范围,根据“¬p∨¬q”是假命题,得到“p∧q”是真命题,求出m的范围即可.
解答 解:若关于命题p:“函数f(x)=$\frac{1}{3}$x3-(4m-1)x2+(15m2-2m-7)x+2在(-∞,+∞)上是增函数”,为真命题;
对f(x)=$\frac{1}{3}$x3-(4m-1)x2+(15m2-2m-7)x+2求导,得:f′(x)=x2-2(4m-1)x+(15m2-2m-7),
已知函数f(x)=$\frac{1}{3}$x3-(4m-1)x2+(15m2-2m-7)x+2在(-∞,+∞)上是增函数,
故f′(x)≥0,
即求使x2-2(4m-1)x+(15m2-2m-7)≥0的m的取值范围,
可以看出函数开口向上,使△≤0即可,
对[-2(4m-1)]2-4(15m2-2m-7)≤0求解,得:2≤m≤4.
若关于命题q:“曲线$\frac{x^2}{5-m}+\frac{y^2}{1+m}=1$表示椭圆”,为真命题;
则$\left\{\begin{array}{l}{\stackrel{5-m>0}{1+m>0}}\\{5-m≠1+m}\end{array}\right.$,解得:-1<m<5,且m≠2,
由题意知,命题“¬p∨¬q”为假,其否定为“p∧q”,是真命题.
所以由$\left\{\begin{array}{l}{2≤m≤4}\\{-1<m<5,m≠2}\end{array}\right.$,解得:m∈(2,4].
可得:实数m的取值范围是:(2,4].
点评 本题考查了复合命题的判断,考查椭圆和二次函数的性质,是一道基础题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 合计 | |
| 男性 | 16 | 14 | 30 |
| 女性 | 44 | 26 | 70 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
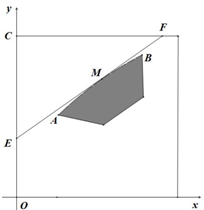 如图,某城市有一个边长为4百米的正方形休闲广场,广场中间阴影部分是一个雕塑群.建立坐标系(单位:百米),则雕塑群的左上方边缘曲线AB是抛物线y2=4x(1≤x≤3,y≥0)的一段.为方便市民,拟建造一条穿越广场的直路EF(宽度不计),要求直路EF与曲线AB相切(记切点为M),并且将广场分割成两部分,其中直路EF左上部分建设为主题陈列区.记M点到OC的距离为m(百米),主题陈列区的面积为S(万平方米).
如图,某城市有一个边长为4百米的正方形休闲广场,广场中间阴影部分是一个雕塑群.建立坐标系(单位:百米),则雕塑群的左上方边缘曲线AB是抛物线y2=4x(1≤x≤3,y≥0)的一段.为方便市民,拟建造一条穿越广场的直路EF(宽度不计),要求直路EF与曲线AB相切(记切点为M),并且将广场分割成两部分,其中直路EF左上部分建设为主题陈列区.记M点到OC的距离为m(百米),主题陈列区的面积为S(万平方米).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com