练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知2是函数f（x）=$\left\{\begin{array}{l}{{log}_{2}（x+m），x≥2}\\{{2}^{x}，x＜2}\end{array}\right.$ 的一个零点，则f[f（4）]的值是（　　）
    A．3B．2C．1D．log23

    分析 根据f（2）=0求出m，再计算f（4），f[f（4）]．

    解答 解：∵2是f（x）的一个零点，∴f（2）=0，
    即log2（2+m）=0，∴m=-1．
    ∴f（4）=log23＜2，
    ∴f[f（4）]=2${\;}^{lo{g}_{2}3}$=3．
    故选：A．

    点评 本题考查了零点的定义，对数的运算性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

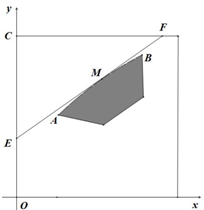    11．如图，某城市有一个边长为4百米的正方形休闲广场，广场中间阴影部分是一个雕塑群．建立坐标系（单位：百米），则雕塑群的左上方边缘曲线AB是抛物线y2=4x（1≤x≤3，y≥0）的一段．为方便市民，拟建造一条穿越广场的直路EF（宽度不计），要求直路EF与曲线AB相切（记切点为M），并且将广场分割成两部分，其中直路EF左上部分建设为主题陈列区．记M点到OC的距离为m（百米），主题陈列区的面积为S（万平方米）．
    （1）当M为EF中点时，求S的值；
    （2）求S的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知一组数据x1，x2，x3，x4，x5的平均数是2，方差是$\frac{1}{3}$，那么另一组数据3x1-2，3x2-2，3x3-2，
    3x4-2，3x5-2的平均数和方差分别是4，3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．复数$\frac{1}{1+2i}$的虚部与实部的和是$-\frac{1}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．将十进制数258化成四进制数是（10002）4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．若函数f（x）=ax3-bx+4，当x=2时，函数f（x）有极值$-\frac{4}{3}$．
    （1）求曲线y=f（x）在点（1，f（1））处的切线方程；
    （2）若方程f（x）=k有3个不同的根，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如表：
    零件的个数x（个）2345
    加工的时间y（小时）2.5344.5
    （1）在给定的坐标系中画出表中数据的散点图；
    （2）求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$，并在坐标系中画出回归直线；
    （3）试预测加工10个零件需要多少时间？
    （可能用到的公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$x，其中$\hat a$、$\hat b$是对回归直线方程$\hat y=a+bx$中系数a、b按最小二乘法求得的估计值）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．曲线f（x）=ln（2x+1）在点（0，f（0））处的切线方程为（　　）
    A．y=xB．y=x+1C．y=2xD．y=2x+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知曲线f（x）=x3-3x及曲线y=f（x）上一点P（1，-2）．
    （I） 求曲线y=f（x）在P点处的切线方程；
    （Ⅱ）求曲线y=f（x）过P点的切线方程．

    查看答案和解析>>

    同步练习册答案