Question

6．若函数f（x）=ax³-bx+4，当x=2时，函数f（x）有极值$-\frac{4}{3}$．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）若方程f（x）=k有3个不同的根，求实数k的取值范围．

Answer 1

分析 （1）根据f（2）=-$\frac{4}{3}$，f′（2）=0列方程解出a，b得出f（x）的解析式，利用导数的几何意义求出切线方程；
（2）求出f（x）的极大值和极小值，则k介于f（x）的极大值与极小值之间．

解答 解：（1）f'（x）=3ax²-b，由题意得$\left\{\begin{array}{l}f'（2）=12a-b=0\\ f（2）=8a-2b+4=-\frac{4}{3}\end{array}\right.$，解得$\left\{\begin{array}{l}a=\frac{1}{3}\\ b=4\end{array}\right.$．
∴$f（x）=\frac{1}{3}{x^3}-4x+4$．f'（x）=x²-4，
∴$f'（1）=-3，f（1）=\frac{1}{3}$，
∴y=f（x）在点（1，f（1））处的切线方程为：$y-\frac{1}{3}=-3（x-1）$，即9x+3y-10=0．
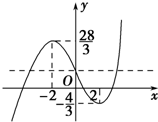
（2）由（1）可得f'（x）=x²-4，令f'（x）=0，得x=2或x=-2．
当x变化时，f'（x），f（x）的变化情况如下表：

x	（-∞，-2）	-2	（-2，2）	2	（2，+∞）
f'（x）	+	0	-	0	+
f（x）	↑	$\frac{28}{3}$	↓	-$\frac{4}{3}$	↑?

∴当x=-2时，f（x）有极大值$\frac{28}{3}$，当x=2，时，f（x）有极小值-$\frac{4}{3}$，
所以函数$f（x）=\frac{1}{3}{x^3}-4x+4$的图象大致如图所示．

若f（x）=k有3个不同的根，所以-$\frac{4}{3}$＜k＜$\frac{28}{3}$．

点评 本题考查了导数的几何意义，导数与函数单调性，极值的关系，属于中档题．