
分析 由k•${C}_{n+1}^{k}$=(n+1)•${C}_{n}^{k-1}$,得$\frac{1}{k}$•${C}_{n}^{k-1}$=$\frac{1}{n+1}$•${C}_{n+1}^{k}$,化简C${\;}_{n}^{0}$+$\frac{1}{2}$C${\;}_{n}^{1}$+$\frac{1}{3}$C${\;}_{n}^{2}$+…+$\frac{1}{n+1}$C${\;}_{n}^{n}$,求出n的值,再求二项式展开式中系数最大的项.
解答 解:由k•${C}_{n+1}^{k}$=(n+1)•${C}_{n}^{k-1}$,得$\frac{1}{k}$•${C}_{n}^{k-1}$=$\frac{1}{n+1}$•${C}_{n+1}^{k}$,
∴C${\;}_{n}^{0}$+$\frac{1}{2}$C${\;}_{n}^{1}$+$\frac{1}{3}$C${\;}_{n}^{2}$+…+$\frac{1}{n+1}$C${\;}_{n}^{n}$
=$\frac{1}{n+1}$•${C}_{n+1}^{1}$+$\frac{1}{n+1}$•${C}_{n+1}^{2}$+$\frac{1}{n+1}$•${C}_{n+1}^{3}$+…+$\frac{1}{n+1}$•${C}_{n+1}^{n+1}$
=$\frac{1}{n+1}$•(${C}_{n+1}^{1}$+${C}_{n+1}^{2}$+${C}_{n+1}^{3}$+…+${C}_{n+1}^{n+1}$)
=$\frac{1}{n+1}$•(2n+1-1)=$\frac{31}{n+1}$,
解得n=4;
∴(1+x)2×4的展开式中系数最大的项为${C}_{8}^{4}$x4=70x4.
故答案为:70x4.
点评 本题考查了二项式定理的应用、组合数的计算公式及其性质,考查了推理能力与计算能力,属于中档题


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
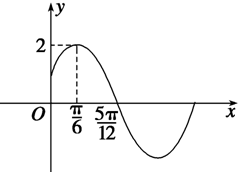 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{4}$] | B. | (0,$\frac{1}{4}$] | C. | (-∞,0]∪[$\frac{1}{4}$,+∞) | D. | (-∞,0)∪($\frac{1}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|1<x<2} | C. | {x|1≤x<2} | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a<$\frac{\sqrt{3}}{3}$ | B. | 0<a≤$\frac{\sqrt{5}}{5}$ | C. | 0<a<$\frac{\sqrt{5}}{5}$ | D. | a≥$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com