
| A. | 0<a<$\frac{\sqrt{3}}{3}$ | B. | 0<a≤$\frac{\sqrt{5}}{5}$ | C. | 0<a<$\frac{\sqrt{5}}{5}$ | D. | a≥$\frac{1}{2}$ |
分析 根据条件判断函数的对称性和周期性,利用函数与方程的关系转化为两个函数的交点个数问题,利用数形结合进行求解即可.
解答 解:由g(3-x)=g(3+x),知即g(x)的图象关于直线x=3对称,
由g(x)=g(x+2)知,g(x)的一个周期T=2.
结合当x∈[1,2]时,g(x)=-2x2+4x-2,
作出g(x)的图象与函数y=loga(x+1)(x>0)的图象,
则方程g(x)=loga(x+1)在(0,+∞)上至少有5个不等的实根等价于
函数g(x)的图象与函数y=loga(x+1)(x>0)的图象至少有5个交点,
如图所示,则$\left\{\begin{array}{l}{0<a<1}\\{lo{g}_{a}(4+1)=lo{g}_{a}5>-2}\end{array}\right.$,
所以0<a<$\frac{\sqrt{5}}{5}$.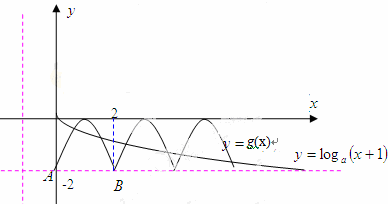
故选:C.
点评 本题主要考查函数与方程的应用,根据条件判断函数的对称性和周期性,利用函数与方程之间的关系转化为两个函数的交点个数问题是解决本题的关键.


科目:高中数学 来源: 题型:解答题
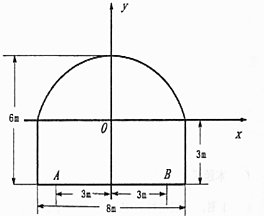 有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)
有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5+6$\sqrt{2}$,$\frac{2}{13}$ | B. | 5+6$\sqrt{2}$,$\frac{1}{5}$ | C. | 20,$\frac{1}{5}$ | D. | 20,$\frac{2}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 合计 | |
| 男性 | 16 | 14 | 30 |
| 女性 | 44 | 26 | 70 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 第4天 | 第10天 | 第18天 | 第25天 |
| 价格(元) | 108 | 120 | 127 | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 16 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com