
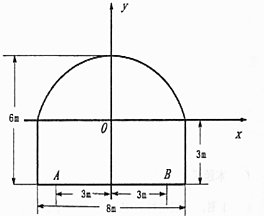
 有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)
有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)分析 (1)由题意设出圆的标准方程,再带点求出未知量即可.
(2)将x的值代入,由此得到限制高度.
解答 解:(1)由题意,设圆的方程为x2+(y-b)2=r2
∵点(4,0),(0,3)在圆上,
∴$\left\{\begin{array}{l}{16+{b}^{2}={r}^{2}}\\{0+(3-b)^{2}={r}^{2}}\end{array}\right.$
∴$\left\{\begin{array}{l}{b=-\frac{7}{6}}\\{{r}^{2}=(\frac{25}{6})^{2}}\end{array}\right.$
故所求方程为:x2+(y+$\frac{7}{6}$)2=($\frac{25}{6}$)2;
(2)由(1)把x=3带入方程得,9+(y+$\frac{7}{6}$)2=($\frac{25}{6}$)2
∴y=$\frac{\sqrt{43}×\sqrt{7}}{6}$≈1.73
因此,限制高度为:3+1.73-0.5=4.2(米)
答:限制高度应为4.2米.
点评 本题考察数形结合的思想,以及待定系数法解决问题,假设出标准方程再求未知量.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
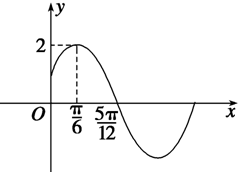 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a<$\frac{\sqrt{3}}{3}$ | B. | 0<a≤$\frac{\sqrt{5}}{5}$ | C. | 0<a<$\frac{\sqrt{5}}{5}$ | D. | a≥$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com