

分析 根据“牛顿调和三角形”的特征,每个数是它下一个行左右相邻两数的和,得出将杨晖三角形中的每一个数Cnr都换成分数$\frac{1}{{({n+1})C_n^r}}$,就得到一个莱布尼兹三角形,从而可求出第n(n≥3)行第3个数字,第6行第2个数
解答 解:(1)第六行第一个数是$\frac{1}{6}$,第二个数设为a(6,2),
那么$\frac{1}{6}+{a_{({6,2})}}=\frac{1}{5}$,所以${a_{({6,2})}}=\frac{1}{5}-\frac{1}{6}=\frac{1}{30}$,
(2)将杨辉三角形中的每一个数$C_n^r$都换成分数$\frac{1}{{({n+1})C_n^r}}$,
就得到一个如图所示的分数三角形,
因为杨辉三角形中的第n(n≥3)行第3个数字是$C_{n-1}^2$,
那么如图三角形数的第n(n≥3)行第3个数字是$\frac{1}{{nC_{n-1}^2}}=\frac{2}{{n({n-1})({n-2})}}$,
故答案为:$\frac{1}{30},\frac{2}{n(n-1)(n-2)}$.
点评 本题考查了学生的归纳推理能力,属于中档题型,学生在课堂上学习过杨辉三角,这个三角形数阵与杨辉三角有关联,所以要熟悉杨辉三角与二项式系数的关系,并且有很好的观察能力,将杨辉三角形中的每一个数$C_n^r$都换成分数$\frac{1}{{({n+1})C_n^r}}$,就得到一个如图所示的分数三角形,并且在转化的时候,组合数的上标和下标不要弄错,仔细解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|a≤2} | B. | {a|a≤1} | C. | {a|a≥1} | D. | {a|a≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m≤\frac{7}{3}$ | B. | m≥-1 | C. | $m≤-1或m≥\frac{7}{3}$ | D. | $-1≤m≤\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{25}{8}$ | D. | $\frac{25}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
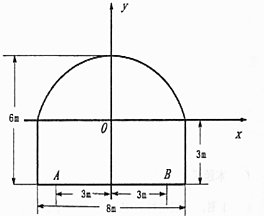 有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)
有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com