
| A. | $\frac{5}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{25}{8}$ | D. | $\frac{25}{16}$ |
分析 先对两个二次函数进行求导,然后设交点坐标,根据它们在一个交点处的切线相互垂直可得到a+b=$\frac{5}{2}$,再由基本不等式可求得最大值.
解答 解:∵y=x2-2x+2,∴y'=2x-2,
∵y=-x2+ax+b,∴y'=-2x+a,
设交点为(x0,y0),
∵它们在一个交点处切线互相垂直,
∴(2x0-2)(-2x0+a)=-1,即4x02-(2a+4)x0+2a-1=0,①
由交点分别代入二次函数式,整理得,
2x02-(2+a)x0+2-b=0,即4x02-(4+2a)x0+4-2b=0,②
由①②整理得 2a-1-4+2b=0,即a+b=$\frac{5}{2}$,(a>0,b>0)
∴ab≤$(\frac{a+b}{2})^{2}$=$\frac{25}{16}$,
∴ab的最大值为$\frac{25}{16}$.
故选:D.
点评 本题主要考查基本不等式的应用,利用导数的几何意义是解决本题的关键,一定要注意用基本不等式的条件“一正、二定、三相等”.综合性较强,运算量较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图(1),在三角形PCD中,AB为其中位线,且2BD=PC=2$\sqrt{6}$,CD=2$\sqrt{2}$,若沿AB将三角形PAB折起,使∠PAD=120°,构成四棱锥P-ABCD,如图(2),E和F分别是棱CD和PC的中点,
如图(1),在三角形PCD中,AB为其中位线,且2BD=PC=2$\sqrt{6}$,CD=2$\sqrt{2}$,若沿AB将三角形PAB折起,使∠PAD=120°,构成四棱锥P-ABCD,如图(2),E和F分别是棱CD和PC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
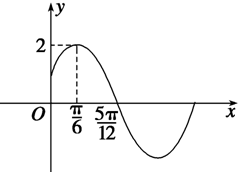 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com