
分析 判断f(x)的单调性,求出f(x)的极值,令极大值大于0,极小值小于0即可求出m的范围.
解答 解:f′(x)=3x2-m,
(1)当m≤0时,f′(x)≥0,∴f(x)在R上是增函数,
∴f(x)在R上不可能有三个零点,
(2)当m>0时,令f′(x)=0解得x=±$\sqrt{\frac{m}{3}}$,
当x<-$\sqrt{\frac{m}{3}}$或x>$\sqrt{\frac{m}{3}}$时f′(x)>0,当-$\sqrt{\frac{m}{3}}$<x<$\sqrt{\frac{m}{3}}$时,f′(x)<0,
∴当x=-$\sqrt{\frac{m}{3}}$时,f(x)取得极大值f(-$\sqrt{\frac{m}{3}}$)=$\frac{2m}{3}\sqrt{\frac{m}{3}}$-1,
当x=$\sqrt{\frac{m}{3}}$时,f(x)取得极小值f($\sqrt{\frac{m}{3}}$)=-$\frac{2m}{3}\sqrt{\frac{m}{3}}$-1,
显然-$\frac{2m}{3}\sqrt{\frac{m}{3}}$-1<0,
∵f(x)在R上有3个零点,∴$\frac{2m}{3}\sqrt{\frac{m}{3}}$-1>0,
解得m>$\frac{3}{\root{3}{4}}$.
故答案为($\frac{3}{\root{3}{4}}$,+∞).
点评 本题考查了函数的极值与零点的关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{25}{8}$ | D. | $\frac{25}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
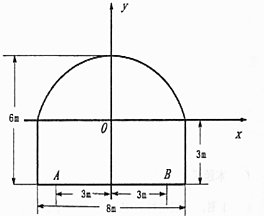 有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)
有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com