
���� �����Ƶ���ֱ��AP�ķ���Ϊy=$\frac{��}{m}$��x-m����ֱ��NP�ķ���Ϊy=-$\frac{4}{��m}$��x+m���������������$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4}$=1���ɴ��������P�Ĺ켣E��
��2���켣E�ķ���Ϊ$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{4}=1$������F��4��0����kΪб�ʵ�ֱ�ߵķ���Ϊy=k��x-4��������$\left\{\begin{array}{l}{y=k��x-4��}\\{\frac{{x}^{2}}{20}+\frac{{y}^{2}}{4}=1}\end{array}\right.$���ã�1+5k2��x2-40k2x+80k2-20=0���ɴ����ø����б�ʽ��Τ�ﶨ�����ҳ���ʽ���㵽ֱ�ߵľ��빫ʽ�����������ʵ��kʹ�ù���F��kΪб�ʵ�ֱ����켣E����M��N���㣬����S��OMN=$\frac{4\sqrt{10}}{3}$��OΪ����ԭ�㣩��
��� �⣺���߳���m��0������$\overrightarrow{a}$=��0��1��������$\overrightarrow{b}$=��m��0����
������A��m��0���Ԧ�$\overrightarrow{a}$+$\overrightarrow{b}$Ϊ����������ֱ���뾭����B��-m��0�����Ԧ�$\overrightarrow{b}$-4$\overrightarrow{a}$Ϊ����������ֱ�߽��ڵ�P�����Цˡ�R��
���$\overrightarrow{a}$+$\overrightarrow{b}$=��m���ˣ�����$\overrightarrow{b}$-4$\overrightarrow{a}$=����m��-4����
��ֱ��AP�ķ���Ϊy=$\frac{��}{m}$��x-m�����٣�ֱ��NP�ķ���Ϊy=-$\frac{4}{��m}$��x+m����
�����٢ڣ���ȥ�ˣ��ã�${y}^{2}=-\frac{4}{{m}^{2}}��{x}^{2}-{m}^{2}��$����$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4}$=1��
�ʵ�m=2ʱ���켣E���ԣ�0��0��ΪԲ�ģ���2Ϊ�뾶��Բ���䷽��Ϊ��x2+y2=4��
��m��2ʱ���켣E����ԭ��Ϊ���ģ��ԣ�$��\sqrt{{m}^{2}-4}$��0��Ϊ�������Բ��
��0��m��2ʱ���켣E����ԭ��Ϊ���ģ��ԣ�0��$��\sqrt{4-{m}^{2}}$��Ϊ�������Բ��
��2����m=2$\sqrt{5}$��F��4��0����
��켣E����ԭ��Ϊԭ�ģ��ԣ���4��0��Ϊ���㣬������Ϊ2$\sqrt{5}$����Բ��
��켣E�ķ���Ϊ$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{4}=1$��
����F��4��0����kΪб�ʵ�ֱ�ߵķ���Ϊy=k��x-4����
����$\left\{\begin{array}{l}{y=k��x-4��}\\{\frac{{x}^{2}}{20}+\frac{{y}^{2}}{4}=1}\end{array}\right.$���ã�1+5k2��x2-40k2x+80k2-20=0��
����0����M��x1��y1����N��x2��y2������x1+x2=$\frac{40{k}^{2}}{1+5{k}^{2}}$��x1x2=$\frac{80{k}^{2}-20}{1+5{k}^{2}}$��
|MN|=$\sqrt{��1+{k}^{2}��[��}{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}]$=$\frac{4\sqrt{5}��1+{k}^{2}��}{1+5{k}^{2}}$��
O��ֱ��y=k��x-4���ľ���d=$\frac{|4k|}{\sqrt{1+{k}^{2}}}$��
��S��OMN=$\frac{4\sqrt{10}}{3}$��OΪ����ԭ�㣩��
��S��OMN=$\frac{1}{2}|MN|•d$=$\frac{8\sqrt{5}|k|•\sqrt{1+{k}^{2}}}{1+5{k}^{2}}$=$\frac{4\sqrt{10}}{3}$��
��������22k4+7k2+1=0��
��=49-88��0����22k4+7k2+1=0�⣬
�����ʵ��kʹ�ù���F��kΪб�ʵ�ֱ����켣E����M��N���㣬����S��OMN=$\frac{4\sqrt{10}}{3}$��OΪ����ԭ�㣩��
���� ���⿼���Ĺ켣������������������ֱ�߷����Ƿ���ڵ��ж��������е��⣬����ʱҪ�������⣬ע������б�ʽ��Τ�ﶨ�����ҳ���ʽ���㵽ֱ�ߵľ��빫ʽ����Բ���ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
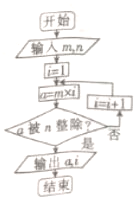
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| y1 | y2 | �ܼ� | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| �ܼ� | a+c | b+d | a+b+c+d |
| A�� | ad-bcԽС��˵��x��y�Ĺ�ϵԽ�� | B�� | ad-bcԽ��˵��x��y�Ĺ�ϵԽ�� | ||
| C�� | ��ad-bc��2Խ��˵��x��y�Ĺ�ϵԽǿ | D�� | ��ad-bc��2ԽС��˵��x��y�Ĺ�ϵԽǿ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com