
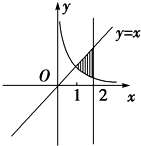
分析 作出曲线y=$\frac{1}{x}$与直线y=x、x=2的图象,求出它们的交点坐标,可得所求面积为函数x-$\frac{1}{x}$在区间[1,2]上的定积分的值,再用定积分计算公式加以运算即可得到本题答案.
解答 解:∵曲线y=$\frac{1}{x}$和曲线y=x的交点为A(1,1),
直线y=x和x=2的交点为B(2,2).
∴曲线y=$\frac{1}{x}$与直线y=x,x=2所围成图形面积为
S=${∫}_{1}^{2}(x-\frac{1}{x})dx$=$(\frac{1}{2}{x}^{2}-lnx){|}_{1}^{2}$=($\frac{1}{2}×{2}^{2}$-ln2)-($\frac{1}{2}×{1}^{2}$-ln1)=$\frac{3}{2}$-ln2.
点评 本题求两条曲线围成的曲边图形的面积,着重考查了定积分的几何意义和积分计算公式等知识,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
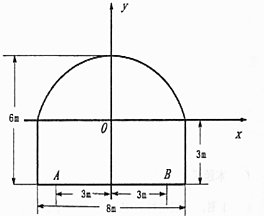 有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)
有一隧道内设为双向两车道公路(道路一侧只能行驶一辆车),其界面由一长方形和一条圆弧组成,如图所示,隧道总宽度为8米,总高度为6米,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米,若行车道总宽度AB为6米(车道AB与隧道两侧墙壁之间各有1米宽的公共设施,禁止行车)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有可能平行 | B. | 有可能垂直 | C. | 一定平行 | D. | 不一定异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=ax3+bx2+cx+d图象与y轴交点坐标为(0,4),其导函数y=f′(x)是以y轴为对称轴的抛物线,大致图象如图所示.
已知函数f(x)=ax3+bx2+cx+d图象与y轴交点坐标为(0,4),其导函数y=f′(x)是以y轴为对称轴的抛物线,大致图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com