练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．正三棱柱ABC-A′B′C′的底面边长为1，高为4，在侧棱BB′有不同的两动点M，N，则AM与NC′（　　）
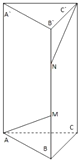
    A．有可能平行B．有可能垂直C．一定平行D．不一定异面

    分析 由题意，设A′B′的中点为D，则C′D⊥平面ABB′A′．确定A′M⊥AM，过D作DN∥A′M，即可得出结论．

    解答 解：由题意，设A′B′的中点为D，则C′D⊥平面ABB′A′．
    设B′M=x，则BM=4-x，
    假设A′M⊥AM，则1+x2+1+（4-x）2=16，
    ∴x2-4x+1=0，
    ∵0＜x＜4，∴x=2±$\sqrt{3}$，
    过D作DN∥A′M，∴AM⊥DN，
    ∴AM与NC′有可能垂直，
    故选：B．

    点评 本题考查线面、线线位置关系，考查学生分析解决问题的能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．分类变量x和y的列联表如下，则（　　）
    y1y2总计
    x1aba+b
    x2cdc+d
    总计a+cb+da+b+c+d
    A．ad-bc越小，说明x与y的关系越弱B．ad-bc越大，说明x与y的关系越弱
    C．（ad-bc）2越大，说明x与y的关系越强D．（ad-bc）2越小，说明x与y的关系越强

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

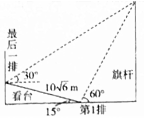    9．某校运动会开幕式上举行升旗仪式，在坡度为15°的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为10$\sqrt{6}$m（如图所示），则旗杆的高度为30m．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．求曲线y=$\frac{1}{x}$与直线y=x，x=2所围成的图形面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若函数f（x）=ex-kx2+（k-e）x有三个不同的零点，则实数k的取值范围是（　　）
    A．（e，+∞）B．（0，e）C．[1，e）D．（0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数f（x）=x3+3x2+2的单调递减区间为（　　）
    A．（-2，+∞）B．（-∞，2）C．（-2，0）D．（0，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．将四位八进制数1000（8）转化为六进制为（　　）
    A．2120（6）B．3120（6）C．2212（6）D．4212（6）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

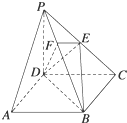    7．如图所示，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，过E点作EF⊥PB交PB于点F．求证：
    （1）PA∥平面EDB；
    （2）PB⊥平面EFD．
    （3）求三棱锥E-BCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知f（x）=ax5+bsinx+cx+2，若f（2）=5，则f（-2）=（　　）
    A．-1B．0C．1D．-5

    查看答案和解析>>

    同步练习册答案