
(本题满分8分)
如图,在直三棱柱ABC-A1B1C1中,E、F分别是A1B、A1C的中点,点D在B1C1上,A1D⊥B1C
求证:(Ⅰ)EF∥平面ABC;
(Ⅱ)平面A1FD⊥平面BB1C1C.

科目:高中数学 来源:2010年吉林省东北师大附中高一下学期期中考试数学 题型:解答题
(本题满分8分)
如图,在正方体 中,
中,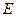 是
是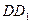 的中点,
的中点,
求证: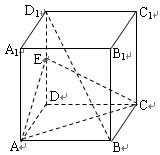
(1)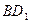 ∥平面
∥平面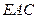 ;
;
(2)求异面直线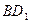 与
与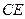 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2011年浙江省苍南县三校高二上学期期中考试数学文卷 题型:解答题
(本题满分8分)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由。

查看答案和解析>>
科目:高中数学 来源:2010年海南省高一期中考试数学试卷 题型:解答题
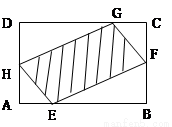
(本题满分8分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(Ⅰ)写出y关于x的函数关系式,并指出这个函数的定义域;
(Ⅱ)当AE为何值时,绿地面积最大?
查看答案和解析>>
科目:高中数学 来源:2010年山东省北校区高二上学期第一次月考数学卷 题型:解答题
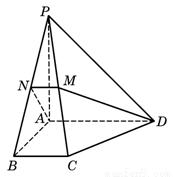
(本题满分8分)如图,在四棱锥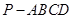 中,底面为直角梯形,
中,底面为直角梯形,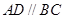 ,
,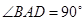 ,
,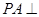 底面
底面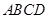 ,且
,且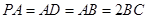 ,
,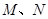 分别为
分别为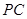 、
、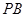 的中点。
的中点。
(Ⅰ)求证: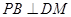 ;
;
(Ⅱ)求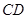 与平面
与平面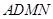 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com