
| A. | 集合{x|x∈Z,|x|<2}的非空真子集的个数是7 | |
| B. | 函数y=($\frac{1}{2}$)${\;}^{{x}^{2}-3x+2}$的单调递减区间是(-∞,$\frac{3}{2}$] | |
| C. | 已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=x-x4,则当x∈(0,+∞)时,f(x)=-x-x4 | |
| D. | 已知f($\frac{2}{x}$+1)=x+3,则f(x)=$\frac{3x-1}{x-1}$ |
分析 A.集合{x|x∈Z,|x|<2}={-1,0,1}的非空真子集的个数是23-2=6,即可判断出正误;
B.利用指数函数、二次函数、复合函数的单调性的判定方法“同增异减”即可得出函数y=($\frac{1}{2}$)${\;}^{{x}^{2}-3x+2}$的单调递减区间是[$\frac{3}{2}$,+∞),即可判断出正误;
C.当x∈(0,+∞)时,则-x∈(-∞,0),根据奇函数的性质可得:f(-x)=-x-(-x)4=-x-x4,利用f(x)=-f(-x)即可判断出正误;
D.由f($\frac{2}{x}$+1)=x+3,令$\frac{2}{x}+1=t$,解得x=$\frac{2}{t-1}$,则f(t)=$\frac{2}{t-1}+3$,化简整理即可判断出正误.
解答 解:A.集合{x|x∈Z,|x|<2}={-1,0,1}的非空真子集的个数是23-2=6,因此不正确;
B.函数y=($\frac{1}{2}$)${\;}^{{x}^{2}-3x+2}$的单调递减区间是[$\frac{3}{2}$,+∞),因此不正确;
C.已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,f(x)=x-x4,则当x∈(0,+∞)时,则-x∈(-∞,0),于是f(-x)=-x-(-x)4=-x-x4,
∴f(x)=-f(-x)=-(-x-x4)=x+x4,因此不正确;
D.由f($\frac{2}{x}$+1)=x+3,令$\frac{2}{x}+1=t$,解得x=$\frac{2}{t-1}$,则f(t)=$\frac{2}{t-1}+3$=$\frac{3t-1}{t-1}$,即f(x)=$\frac{3x-1}{x-1}$(x≠1),正确.
故选:D.
点评 本题考查了简易逻辑的判定方法、集合的性质、函数的奇偶性单调性解析式,考查了推理能力与计算能力,属于中档题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | e | D. | e+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
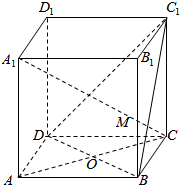 已知在正方体ABCD-A1B1C1D1中,O是DB的中点,直线A1C交平面C1BD于点M,判断下列结论是否正确:
已知在正方体ABCD-A1B1C1D1中,O是DB的中点,直线A1C交平面C1BD于点M,判断下列结论是否正确:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com