练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知a∈R，b∈R，且a≠b，下列结论正确的是(　　)

    (A)a2＋3ab>2b2　　　　　(B)a5＋b5>a3b2＋a2b3

    (C)a2＋b2≥2(a－b－1)  (D)＋>2

    C.对于选项A，(a2＋3ab)－2b2＝(a＋b)2－b2>0不恒成立，故A不正确；

    对于选项B，(a5＋b5)－(a3b2＋a2b3)

    ＝(a5－a3b2)＋(b5－a2b3)

    ＝a3(a2－b2)－b3(a2－b2)

    ＝(a2－b2)(a3－b3)＝(a－b)2(a＋b)(a2＋ab＋b2).

    ∵(a－b)2>0，a2＋ab＋b2

    ＝(a＋)2＋b2>0，

    而a＋b的符号是不确定的，故差值符号不能确定，因此B不正确；

    对于选项C，(a2＋b2)－2(a－b－1)＝a2－2a＋b2＋2b＋2＝(a－1)2＋(b＋1)2≥0，故a2＋b2≥2(a－b－1)，C正确；当a、b异号时，选项D不正确，故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知a∈R，b∈R，且
    b≥a
    b≤a+1
    b≥-2a+2
    ，则
    9a2+b2
    ab
    的最大值与最小值之和为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a∈R，b∈R，A={2，4，x2-5x+9}，B={3，x2+ax+a}，C={x2+（a+1）x-3，1}：求
    （1）A={2，3，4}的x值；
    （2）使2∈B，B?A，求a，x的值；
    （3）使B=C的a，x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a∈R，b∈R，且a+2b=4，则ab的最大值是(    )

    A.2                  B.                   C.4                D.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知a∈R，b∈R，A={2，4，x2-5x+9}，B={3，x2+ax+a}，C={x2+（a+1）x-3，1}：求
    （1）A={2，3，4}的x值；
    （2）使2∈B，B?A，求a，x的值；
    （3）使B=C的a，x的值．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年福建省福州一中高三（上）期末数学试卷（理科）（解析版） 题型：选择题

    已知a∈R，b∈R，且，则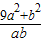的最大值与最小值之和为（ ）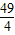
    A．18
    B．16
    C．14
    D．

    查看答案和解析>>

    同步练习册答案