
已知椭圆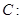
 的左焦点为
的左焦点为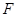 ,左、右顶点分别为
,左、右顶点分别为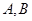 ,过点
,过点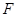 且倾斜角为
且倾斜角为 的直线
的直线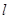 交椭圆于
交椭圆于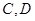 两点,椭圆
两点,椭圆 的离心率为
的离心率为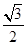 ,
,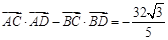 .
.
(1)求椭圆 的方程;
的方程;
(2)若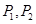 是椭圆上不同两点,
是椭圆上不同两点,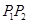
 轴,圆
轴,圆 过点
过点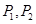 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆 内,则称圆
内,则称圆 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆 是否存在过点
是否存在过点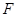 的内切圆?若存在,求出点
的内切圆?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(1)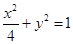 ;(2)存在
;(2)存在
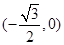
解析试题分析:(1)由离心率为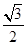 ,倾斜角为
,倾斜角为 的直线
的直线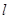 交椭圆于
交椭圆于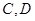 两点,
两点,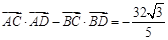 .通过联立直线方程与椭圆的方程,可求得
.通过联立直线方程与椭圆的方程,可求得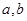 的值.即可得结论.
的值.即可得结论.
(2)依题意可得符合要求的圆E,即为过点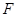 ,
, 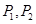 的三角形的外接圆.所以圆心在x轴上.根据题意写出圆E的方程.由于圆的存在必须要符合,椭圆上的点到点
的三角形的外接圆.所以圆心在x轴上.根据题意写出圆E的方程.由于圆的存在必须要符合,椭圆上的点到点 距离的最小值是
距离的最小值是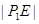 ,结合图形可得圆心E在线段
,结合图形可得圆心E在线段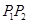 上,半径最小.又由于点F已知,即可求得结论.
上,半径最小.又由于点F已知,即可求得结论.
试题解析:(1)因为离心率为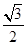 ,所以
,所以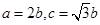 ,
,
所以椭圆方程可化为: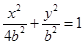 ,直线
,直线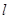 的方程为
的方程为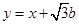 , 2分
, 2分
由方程组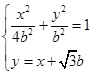 ,得:
,得: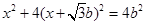 ,即
,即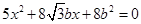 , 4分
, 4分
设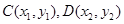 ,则
,则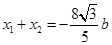 , 5分
, 5分
又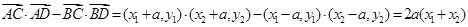 ,
,
所以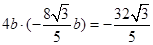 ,所以
,所以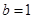 ,椭圆方程是
,椭圆方程是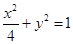 ; 7分
; 7分
(2)由椭圆的对称性,可以设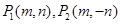 ,点
,点 在
在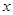 轴上,设点
轴上,设点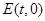 ,
,
则圆 的方程为
的方程为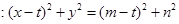 ,
,
由内切圆定义知道,椭圆上的点到点 距离的最小值是
距离的最小值是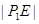 ,
,
设点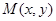 是椭圆
是椭圆 上任意一点,则
上任意一点,则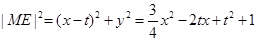 , 9分
, 9分
当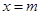 时,
时,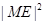 最小,所以
最小,所以 ① 10分
① 10分
又圆 过点
过点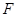 ,所以
,所以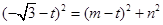 ② 11分
② 11分
点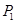 在椭圆上,所以
在椭圆上,所以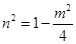 ③ 12分
③ 12分
由①②③解得: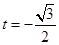 或
或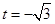 ,
,
又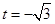 时,
时,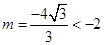 ,不合,
,不合,
综上:椭圆 存在符合条件的内切圆,点
存在符合条件的内切圆,点 的坐标是
的坐标是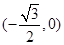 . 13分
. 13分
考点:1.待定系数求椭圆方程.2.函数的最值.3.方程的思想解决解决解几问题.3.归纳化归的思想.4.运算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)= 在(0,1]上解的个数.
在(0,1]上解的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
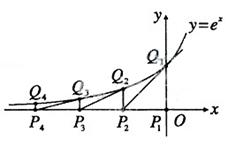
如图,从点P1(0,0)作 轴的垂线交曲线
轴的垂线交曲线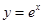 于点
于点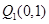 ,曲线在
,曲线在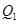 点处的切线与
点处的切线与 轴交于点
轴交于点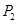 .再从
.再从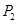 做
做 轴的垂线交曲线于点
轴的垂线交曲线于点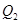 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: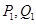 ;
;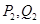 ;…;
;…; ,记
,记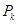 点的坐标为
点的坐标为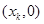 (
(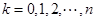 ).
).
(1)试求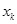 与
与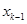 的关系(
的关系(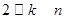 );
);
(2)求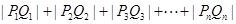 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数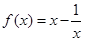 .
.
(1)判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)用定义证明函数 在区间
在区间 上为增函数;
上为增函数;
(3)若函数 在区间
在区间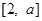 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于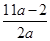 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知f(x)=x+ -3,x∈[1,2].
-3,x∈[1,2].
(1)当b=2时,求f(x)的值域;
(2)若b为正实数,f(x)的最大值为M,最小值为m,且满足M-m≥4,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com