
已知函数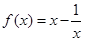 .
.
(1)判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)用定义证明函数 在区间
在区间 上为增函数;
上为增函数;
(3)若函数 在区间
在区间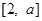 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于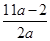 ,求
,求 的取值范围.
的取值范围.
(1)证明见解析;(2)证明见解析;(3)[4,+∞).
解析试题分析:(1)利用奇偶性定义可证;(2)利用单调性定义可证;(3)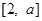 在单调递增区间内,由题意可得关于
在单调递增区间内,由题意可得关于 的不等式,解不等式即可.
的不等式,解不等式即可.
试题解析:
解:(1)函数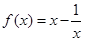 是奇函数, 1分
是奇函数, 1分
∵函数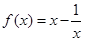 的定义域为
的定义域为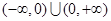 ,在
,在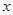 轴上关于原点对称, 2分
轴上关于原点对称, 2分
且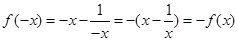 , 3分
, 3分
∴函数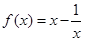 是奇函数. 4分
是奇函数. 4分
(2)证明:设任意实数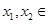
 ,且
,且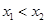 , 5分
, 5分
则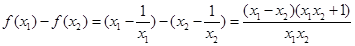 , 6分
, 6分
∵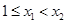 ∴
∴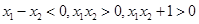 , 7分
, 7分
∴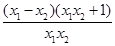 <0 , 8分
<0 , 8分
∴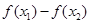 <0,即
<0,即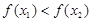 , 9分
, 9分
∴函数 在区间
在区间 上为增函数. 10分
上为增函数. 10分
(3)∵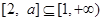 ,
,
∴函数 在区间
在区间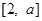 上也为增函数. 11分
上也为增函数. 11分
∴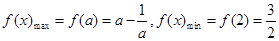 , 12分
, 12分
若函数 在区间
在区间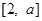 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于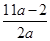 ,
,
则 , 13分
, 13分
∴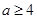 ,
,
∴ 的取值范围是[4,+∞). 14分
的取值范围是[4,+∞). 14分
考点:函数的单调性,奇偶性,最值.


科目:高中数学 来源: 题型:解答题
已知定义在区间(0,+∞)上的函数f(x)满足f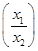 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,求f(x)在[2,9]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2x+k·2-x,k∈R.
(1)若函数f(x)为奇函数,求实数k的值;
(2)若对任意的x∈[0,+∞)都有f(x)>2-x成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆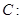
 的左焦点为
的左焦点为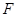 ,左、右顶点分别为
,左、右顶点分别为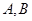 ,过点
,过点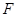 且倾斜角为
且倾斜角为 的直线
的直线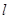 交椭圆于
交椭圆于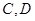 两点,椭圆
两点,椭圆 的离心率为
的离心率为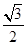 ,
,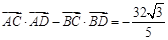 .
.
(1)求椭圆 的方程;
的方程;
(2)若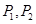 是椭圆上不同两点,
是椭圆上不同两点,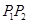
 轴,圆
轴,圆 过点
过点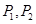 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆 内,则称圆
内,则称圆 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆 是否存在过点
是否存在过点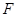 的内切圆?若存在,求出点
的内切圆?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种树苗栽种时高度为A(A为常数)米,栽种n年后的高度记为f(n).经研究发现f(n)近似地满足f(n)=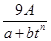 ,其中
,其中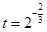 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
(1)栽种多少年后,该树木的高度是栽种时高度的8倍;
(2)该树木在栽种后哪一年的增长高度最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com