
已知函数f(x)=2x+k·2-x,k∈R.
(1)若函数f(x)为奇函数,求实数k的值;
(2)若对任意的x∈[0,+∞)都有f(x)>2-x成立,求实数k的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=-x2+2ex+m-1,g(x)=x+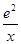 (x>0).
(x>0).
(1)若g(x)=m有实数根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).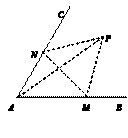
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,从点P1(0,0)作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,曲线在
,曲线在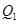 点处的切线与
点处的切线与 轴交于点
轴交于点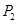 .再从
.再从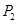 做
做 轴的垂线交曲线于点
轴的垂线交曲线于点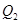 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: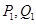 ;
;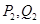 ;…;
;…; ,记
,记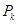 点的坐标为
点的坐标为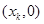 (
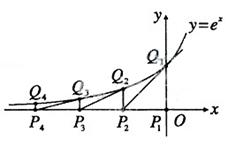
(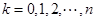 ).
).
(1)试求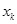 与
与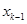 的关系(
的关系(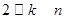 );
);
(2)求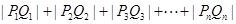 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=log3(9x)·log3(3x), ≤x≤9.
≤x≤9.
(1)若m=log3x,求m的取值范围.
(2)求f(x)的最值,并给出最值时对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数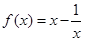 .
.
(1)判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)用定义证明函数 在区间
在区间 上为增函数;
上为增函数;
(3)若函数 在区间
在区间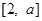 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于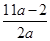 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知抛物线 的焦点为
的焦点为 ,点
,点 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4, .
.
(1)求抛物线的方程;
(2)设点 是抛物线上的两点,
是抛物线上的两点,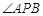 的角平分线与
的角平分线与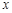 轴垂直,求
轴垂直,求 的面积最大时直线
的面积最大时直线 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com